Neste tópico
- Estimativa pontual de um percentil para uma determinada porcentagem
- Erro padrão de um percentil para uma determinada porcentagem
- Intervalo de confiança fiducial de um percentil para uma determinada porcentagem
- Intervalo de confiança fiducial da probabilidade de falha ou da probabilidade de sobrevivência em um determinado valor de estresse
- Referências
Estimativa pontual de um percentil para uma determinada porcentagem
O ponto do percentil p , xp, é o nível de estresse necessário para uma resposta p.
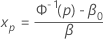
Para encontrar a estimativa de xp, use a seguinte fórmula:
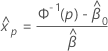
em que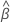 
e 
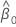são as estimativas de máxima verossimilhança de 
e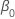 
.
As distribuições de localização de log para Probit Analysis são as distribuições lognormal, loglogística e Weibull. Para distribuições de localização de log, as fórmulas anteriores estimam o percentil na escala de log. Para estimar o percentil na escala dos dados com essas distribuições, use a fórmula a seguir.
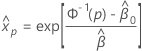
Erro padrão de um percentil para uma determinada porcentagem
O cálculo do erro padrão de um percentil usa o método delta. O erro padrão do percentil estimado tem a seguinte fórmula.
onde a variância de 
tem a seguinte forma:
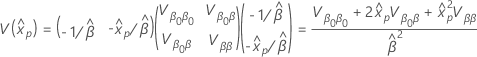
e a matriz de variância-covariância d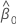e 
e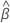 
tem a seguinte forma:
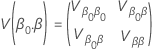
As distribuições de localização de log para Probit Analysis são as distribuições lognormal, loglogística e Weibull. Para distribuições de localização de log, as fórmulas anteriores estimam a variância de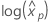 
. Definições da variância e da matriz de variância-covariância em termos de 
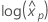seguir.
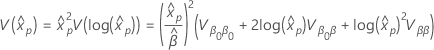
Intervalo de confiança fiducial de um percentil para uma determinada porcentagem
Os dois lados, 100 (1 - 
) para 
É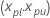 
com as seguintes equações.
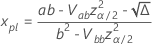
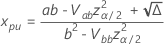
em que
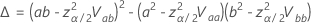
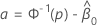
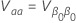
As distribuições de localização de log para Probit Analysis são as distribuições lognormal, loglogística e Weibull. Para distribuições de localização de log, as fórmulas anteriores estimam o intervalo na escala de log. Para estimar o intervalo na escala dos dados, exponenciar os limites de confiança nas fórmulas anteriores.
Intervalo de confiança fiducial da probabilidade de falha ou da probabilidade de sobrevivência em um determinado valor de estresse
Os dois lados, 100 (1 - 
) para a probabilidade de falha,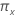 
, É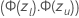 
. Para a probabilidade de sobrevivência, 
, o intervalo é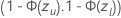 
. As fórmulas a seguir fornecem os cálculos.
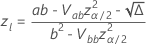
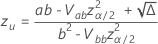
em que
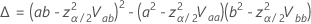
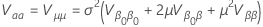
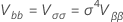
e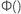 
é a função de distribuição cumulativa da distribuição para a análise.
As distribuições de localização de log para Probit Analysis são as distribuições lognormal, loglogística e Weibull. Para distribuições de localização de log, substitua a definição a seguir.
Referências
A derivação dos intervalos de confiança fiducial usa o teorema de Fieller. O teorema de Fileler está na seguinte referência.
Finney, D. J. (1971). Probit analysis, (Third edition), London: Cambridge University Press.
Para obter mais informações sobre o modelo probit e a estimativa de percentis, consulte a referência a seguir.
Cox, D. R. and Snell, E. J. (1989). The analysis of binary data (Second edition), London: Chapman & Hall.
