Um engenheiro de para-brisas de aviões deseja investigar o quão bem os para-brisas podem suportar impactos de projéteis em um intervalo de velocidades. O engenheiro submete uma amostra aleatória de para-brisas a projéteis em uma das oito velocidades e registra se eles resistiram ao impacto.
O engenheiro realiza a análise por probito para determinar a variedade de velocidades em que uma determinada porcentagem dos para-brisas será romperá quando submetidos ao impacto do projétil.
- Abra os dados das amostras, TensãoParabrisa.MWX.
- Selecione .
- Selecione Resposta no formato evento/ensaio.
- Em Número de eventos, insira Quebras.
- Em Número de ensaios, insira N.
- Em Estresse (estímulo), insira Estresse.
- Exemplo Distribuição assumida, selecione Normal.
- Clique em OK.
Interpretar os resultados
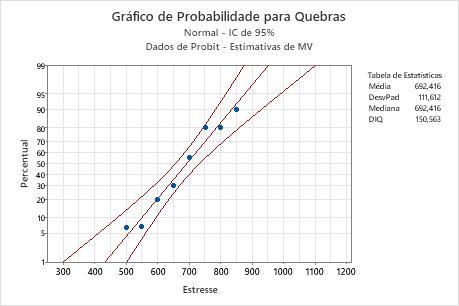
Para avaliar o ajuste de distribuição, o engenheiro utiliza um nível de significância de 0,1. Os valores de p de qualidade de ajuste (0,977 e 0,975) são maiores do que o nível de significância, e os pontos no gráfico de probabilidade caem ao longo de uma linha aproximadamente reta. Portanto, o engenheiro pode assumir que o modelo de distribuição normal fornece um bom ajuste para os dados.
Para avaliar os efeitos significativos, o engenheiro utiliza um nível de significância de 0,05. Como o valor de p para o Estresse (0,000) é menor do que o nível de significância (0,05), o engenheiro conclui que a velocidade do projétil produz um efeito estatisticamente significativo sobre o fato de o para-brisas quebrar ou não.
A tabela de percentis indica que o engenheiro pode ter 95% de certeza de que 1% dos para-brisas falharão a uma velocidade entre 300,019 mph e 501,649 mph.
Informações da Resposta
| Variável | Valor | Contagem |
|---|---|---|
| Quebras | Evento | 37 |
| Não-evento | 52 | |
| N | Total | 89 |
Tabela de Regressão
| Variável | Coef. | Erro Padrão | Z | P |
|---|---|---|---|---|
| Constante | -6,20376 | 1,06565 | -5,82 | 0,000 |
| Estresse | 0,0089596 | 0,0015615 | 5,74 | 0,000 |
| Natural | ||||
| Resposta | 0 |
Testes de Qualidade de Ajuste
| Método | Qui-Quadrado | GL | P |
|---|---|---|---|
| Pearson | 1,19972 | 6 | 0,977 |
| Deviance | 1,22858 | 6 | 0,975 |
Estimativas dos Parâmetros
| IC Normal de 95,0% | ||||
|---|---|---|---|---|
| Parâmetro | Estimativa | Erro Padrão | Inferior | Superior |
| Média | 692,416 | 18,3649 | 656,421 | 728,410 |
| DesvPad | 111,612 | 19,4518 | 79,3167 | 157,058 |
Tabela de Percentis
| IC Fiducial de 95,0% | ||||
|---|---|---|---|---|
| Percentual | Percentil | Erro Padrão | Inferior | Superior |
| 1 | 432,767 | 45,8542 | 300,019 | 501,649 |
| 2 | 463,192 | 41,0355 | 345,266 | 525,291 |
| 3 | 482,496 | 38,0450 | 373,838 | 540,427 |
| 4 | 497,018 | 35,8391 | 395,242 | 551,902 |
| 5 | 508,830 | 34,0781 | 412,585 | 561,304 |
| 6 | 518,884 | 32,6067 | 427,289 | 569,364 |
| 7 | 527,699 | 31,3403 | 440,133 | 576,480 |
| 8 | 535,592 | 30,2277 | 451,589 | 582,896 |
| 9 | 542,771 | 29,2352 | 461,967 | 588,771 |
| 10 | 549,379 | 28,3398 | 471,482 | 594,217 |
| 20 | 598,480 | 22,4304 | 540,595 | 636,280 |
| 30 | 633,886 | 19,4337 | 587,639 | 669,400 |
| 40 | 664,139 | 18,1881 | 624,815 | 700,723 |
| 50 | 692,416 | 18,3649 | 656,409 | 733,152 |
| 60 | 720,692 | 19,8068 | 685,039 | 768,545 |
| 70 | 750,945 | 22,4716 | 713,104 | 808,979 |
| 80 | 786,351 | 26,5977 | 743,723 | 858,524 |
| 90 | 835,453 | 33,3805 | 783,926 | 929,497 |
| 91 | 842,060 | 34,3538 | 789,210 | 939,174 |
| 92 | 849,239 | 35,4233 | 794,925 | 949,712 |
| 93 | 857,132 | 36,6126 | 801,183 | 961,326 |
| 94 | 865,948 | 37,9558 | 808,140 | 974,328 |
| 95 | 876,002 | 39,5048 | 816,041 | 989,192 |
| 96 | 887,814 | 41,3455 | 825,280 | 1006,70 |
| 97 | 902,335 | 43,6350 | 836,585 | 1028,27 |
| 98 | 921,639 | 46,7171 | 851,535 | 1057,03 |
| 99 | 952,065 | 51,6465 | 874,954 | 1102,50 |