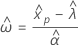Percentis e erros padrão dos percentis
Percentis são estimativas dos tempos em que uma determinada porcentagem da população apresentou falhas. Por padrão, o Minitab exibe tabelas de percentis para análise de distribuição paramétrica para percentis comuns.
Os erros padrão para as estimativas dos percentis são a raiz quadrada das variâncias.
 ,
,  ,
,  ,
,  ,
,  ,
, 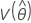 ,
, 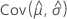 ,
, 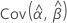 ,
, 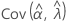 ,
, 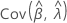 ,
, 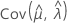 e
e 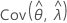 denota as variâncias e covariâncias dos MLEs de μ, σ, α, β, θ e λ, que são retirados do elemento apropriado da inversa da matriz de informação de Fisher.
denota as variâncias e covariâncias dos MLEs de μ, σ, α, β, θ e λ, que são retirados do elemento apropriado da inversa da matriz de informação de Fisher.
As fórmulas utilizadas para as estimativas de percentis e variâncias para cada distribuição são as seguintes:
Menor valor extremo
- Percentil
-
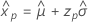
- Variância
-
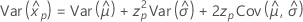
Weibull
- Percentil
-

- Variância
-
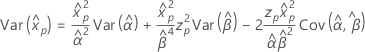
Weibull com 3 parâmetros
- Percentil
-

- Variância
-
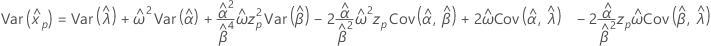
Exponencial
- Percentil
-

- Variância
-

Exponencial com 2 parâmetros
- Percentil
-

- Variância
-
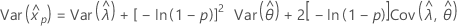
Normal
- Percentil
-
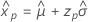
- Variância
-
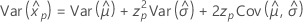
Lognormal
- Percentil
-

- Variância
-
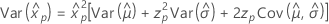
Lognormal para 3 parâmetros
- Percentil
-

- Variância
-
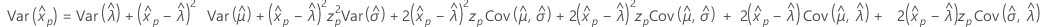
Logística
- Percentil
-
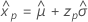
- Variância
-
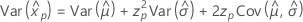
Loglogística
- Percentil
-
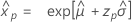
- Variância
-
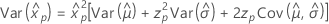
Loglogística para 3 parâmetros
- Percentil
-

- Variância
-

Notação
| Termo | Descrição |
|---|---|
| zp |
o fda inverso da distribuição normal avaliado em p (o po percentil da distribuição padrão) |
Limite de confiança para percentis
| Distribuição | Limites de confiança |
|---|---|
|
Menor valor extremo Normal Logística |
  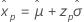 |
|
Weibull Exponencial Lognormal Loglogística |
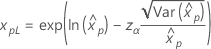 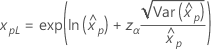 onde |
|
Weibull com 3 parâmetros Exponencial com 2 parâmetros Lognormal para 3 parâmetros Loglogística para 3 parâmetros |
Se λ < 0:   Se λ 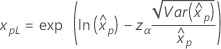 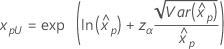 onde |
Para os cálculos da variância do xp estimado, consulte a seção "Percentis e erro padrão de percentis".
Notação
| Termo | Descrição |
|---|---|
| zα | o 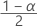 valor crítico superior para a distribuição normal padrão em que 100α % é o nível de confiança. valor crítico superior para a distribuição normal padrão em que 100α % é o nível de confiança. |