Neste tópico
Gráfico de probabilidade
Use o gráfico de probabilidade para avaliar o quão bem a distribuição selecionada ajusta seus dados. Se os pontos acompanham de perto a linha ajustada, é possível assumir que a distribuição ajusta os dados razoavelmente bem.
- Os pontos do gráfico são os percentis estimados com base em um método não paramétrico, que não depende de nenhuma distribuição. Quando o ponteiro do mouse é mantido sobre um ponto de dados, o Minitab exibe o tempo de falha observado e a probabilidade acumulada estimada.
- A linha ajustada (linha central) baseia-se na distribuição ajustada. Quando o ponteiro do mouse é mantido sobre a linha ajustada, o Minitab exibe uma tabela de percentis para várias porcentagens.
- A linha à esquerda conecta os limites inferiores nos intervalos de confiança para cada percentil. A linha à direita conecta os limites superiores nos intervalos de confiança para cada percentil.
Saída do exemplo
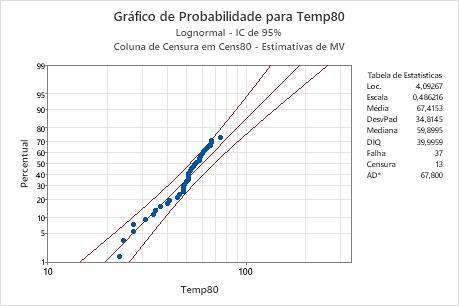
Interpretação
Para a amostra Temp80 dos dados de enrolamento do motor, os pontos parecem seguir a linha ajustada. Portanto, é possível supor que a distribuição lognormal seja uma escolha adequada para os dados. A linha ajustada baseia-se em uma distribuição lognormal com a localização = 4,09267 e escala = 0,486216.
Gráfico de sobrevivência
O gráfico de sobrevivência mostra a probabilidade de que o item irá sobreviver até um determinado momento. Portanto, o gráfico de sobrevivência mostra a confiabilidade do produto ao longo do tempo.
- A linha central é a confiabilidade estimada ao longo do tempo.
- A linha à direita conecta os limites superiores para a confiabilidade em cada ponto de tempo. A linha à esquerda conecta os limites inferiores para a confiabilidade em cada ponto do tempo.
Quando você mantém o ponteiro do mouse sobre a curva de sobrevivência, o Minitab exibe uma tabela de tempos e probabilidades de sobrevivência.
Use esse gráfico somente quando a distribuição ajustar os dados de forma adequada. Se a distribuição ajustar mal os dados, estas estimativas serão imprecisas. Use o gráfico de identificação de distribuição, gráfico de probabilidade e as medições de qualidade do ajuste para determinar se a distribuição ajusta os dados adequadamente.
Saída do exemplo
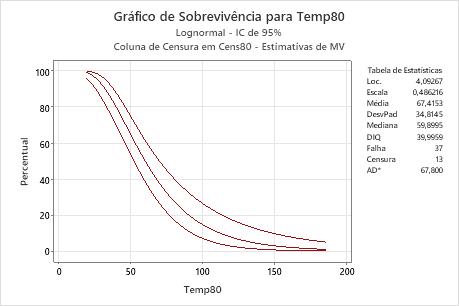
Interpretação
Para os dados dos enrolamentos do motor, a probabilidade de os enrolamentos de motores sobreviverem a uma temperatura de 80 °C durante pelo menos 50 horas é de cerca de 60%. A função de sobrevivência baseia-se na distribuição lognormal com a localização = 4,09267 e escala = 0,486216.
Gráfico de falhas acumuladas
Para descrever a confiabilidade do produto em termos de quando o produto falha, o gráfico de falhas acumuladas exibe a porcentagem acumulada de itens que falham por um determinado tempo, t. A função de falhas acumuladas representa 1 - função de sobrevivência.
- A linha central é a porcentagem de falhas acumuladas estimada ao longo do tempo.
- A linha à direita conecta os limites inferiores para a porcentagem de falhas acumuladas em cada ponto do tempo. A linha à esquerda conecta os limites superiores para a porcentagem de falhas acumuladas em cada ponto de tempo.
Quando você mantém o ponteiro do mouse sobre a curva, o Minitab exibe a probabilidade de falhas acumuladas e o tempo de falha.
Use esse gráfico somente quando a distribuição ajustar os dados de forma adequada. Se a distribuição ajustar mal os dados, estas estimativas serão imprecisas. Use o gráfico de identificação de distribuição, gráfico de probabilidade e as medições de qualidade do ajuste para determinar se a distribuição ajusta os dados adequadamente.
Saída do exemplo
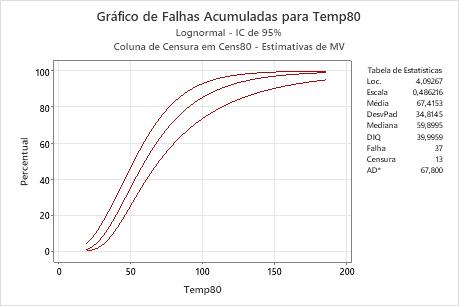
Interpretação
Para os dados dos enrolamentos do motor, a probabilidade de os enrolamentos de motores falharem em torno de 70 horas à temperatura de 80 °C é de aproximadamente 60%. A função de falhas acumuladas baseia-se na distribuição lognormal com a localização = 4,09267 e escala = 0,486216.
Gráfico de risco
- Diminuindo: os itens são menos propensos a falhar com a idade. Um risco decrescente normalmente acontece no início do período de vida de um produto.
- Constante: os itens falham a uma taxa constante. Um risco constante normalmente acontece durante a "vida útil" de um produto quando as falhas ocorrem de forma aleatória.
- Aumentando: os itens são mais propensos a falhar com a idade. Um risco crescente normalmente acontece nas fases posteriores da vida útil de um produto, como no desgaste.
A forma da função de risco é determinada com base nos dados e na distribuição escolhida. Quando você mantém o ponteiro do mouse sobre a curva de risco, o Minitab exibe uma tabela de tempos de falha e taxas de risco.
Use esse gráfico somente quando a distribuição ajustar os dados de forma adequada. Se a distribuição ajustar mal os dados, estas estimativas serão imprecisas. Use o gráfico de identificação de distribuição, gráfico de probabilidade e as medições de qualidade do ajuste para determinar se a distribuição ajusta os dados adequadamente.
Saída do exemplo
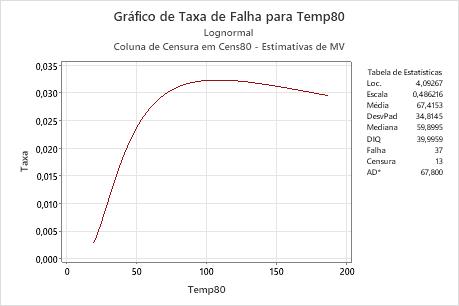
Interpretação
Para a variável Temp80 dos dados de enrolamentos do motor, a função de risco é baseada na distribuição lognormal com a localização = 4,09267 e escala = 0,486216. A uma temperatura de 80 °C, a taxa de risco aumenta até aproximadamente 100 horas, diminuindo lentamente.
Gráficos do modo de múltiplas falhas
Para os dados de múltiplas falhas, o Minitab exibe gráficos para cada modo de falha.
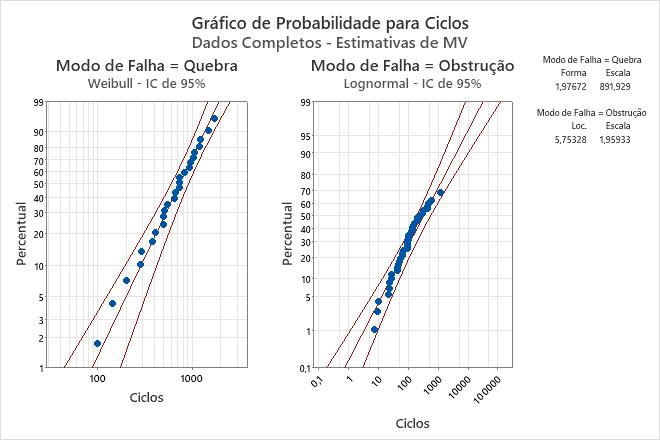
- Use o gráfico de probabilidade para avaliar o quão bem a distribuição selecionada ajusta seus dados. Se os pontos seguirem a linha ajustada de maneira próxima, use essa distribuição para modelar os dados.
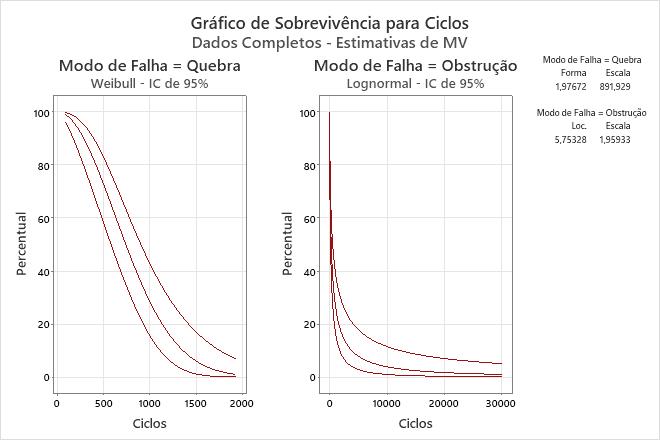
- Use o gráfico de sobrevivência para avaliar a probabilidade de que o item sobreviva até um determinado momento. Portanto, o gráfico de sobrevivência mostra a confiabilidade do produto ao longo do tempo.
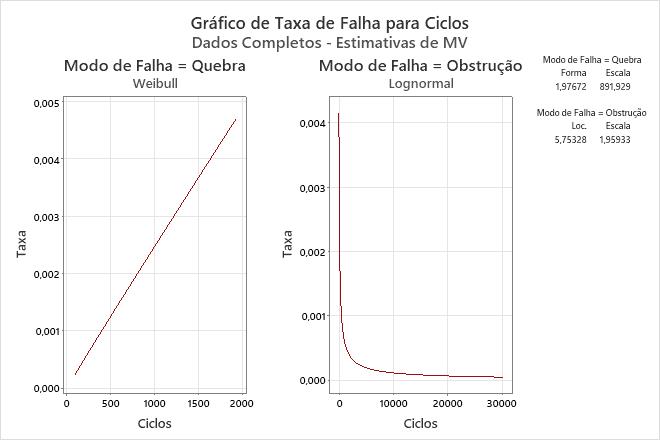
- Use a função de risco para fornecer a probabilidade de falha como uma função do tempo que uma unidade durou (a taxa de falha instantânea em um determinado momento, t). O gráfico de risco mostra a tendência da taxa de falha ao longo do tempo.
Saída do exemplo
Interpretação
- Forma = 1,97672 e escala = 891,929 para as quebras do braço de pulverização
- Localização = 5,75328 e escala = 1,95933 para as obstruções do braço de pulverização
A probabilidade de que os braços de pulverização irão sobreviver a quebras durante 200 ciclos é de 95%, e que eles vão sobreviver a obstruções por 1500 ciclos é de cerca de 20%.
A taxa de risco para quebras aumenta um pouco ao longo do tempo, mas para obstruções diminui ao longo do tempo.
