Neste tópico
Gráfico de sobrevivência – Método de estimativa atuarial
O gráfico de sobrevivência mostra a probabilidade de que o item irá sobreviver até um determinado momento. Portanto, o gráfico mostra a confiabilidade do produto ao longo do tempo. O eixo Y mostra a probabilidade de sobrevivência e o eixo X mostra a medição confiabilidade (tempo, número de cópias, milhas percorridas).
Para uma análise não paramétrica, o gráfico de sobrevivência é uma função de etapas com etapas nos pontos extremos de cada intervalo. Neste exemplo, a função é calculada com o método de estimativa atuarial.
Saída do exemplo
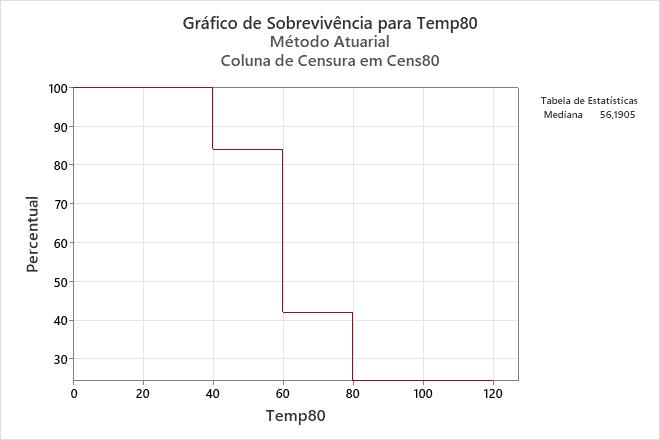
Interpretação
Para os enrolamentos de motor em funcionamento a 80° C, a probabilidade de que um enrolamento sobreviva até 60 horas é de 0,42.
Gráfico de falhas acumuladas – método de estimativa atuarial
O gráfico de falhas acumuladas representa a probabilidade de que o item irá falhar depois de determinado tempo. Portanto, o gráfico mostra a probabilidade de falha do produto ao longo do tempo. O eixo Y mostra a probabilidade de falha e o eixo X mostra a medição confiabilidade (tempo, número de cópias, milhas percorridas).
Para uma análise não paramétrica, o gráfico falhas acumuladas é uma função de etapas com etapas nos pontos extremos de cada intervalo. Neste exemplo, a função é calculada com o método de estimativa atuarial.
Saída do exemplo
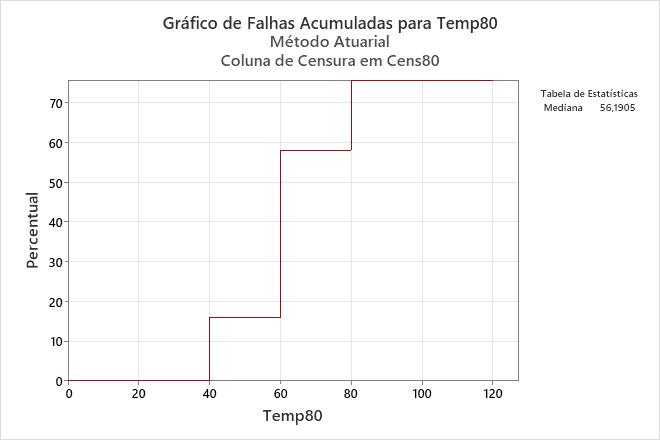
Interpretação
Para os enrolamentos de motor em funcionamento a 80° C, a probabilidade de que um enrolamento falhe em 60 horas ou antes é de 0,58.
Gráfico de riscos – Método de estimativa atuarial
A função de risco proporciona uma medida de probabilidade de falha como uma função de quantidade tempo em que uma unidade tenha sobrevivido. Você pode usar o gráfico de riscos não paramétrico para ajudar a determinar qual distribuição é apropriada para modelar os dados, caso decida usar métodos de estimativa paramétricos.
Para uma análise não paramétrica, o gráfico de riscos é uma função de etapas com etapas nos pontos médios de cada intervalo. Neste exemplo, a função é calculada com o método de estimativa atuarial.
Saída do exemplo
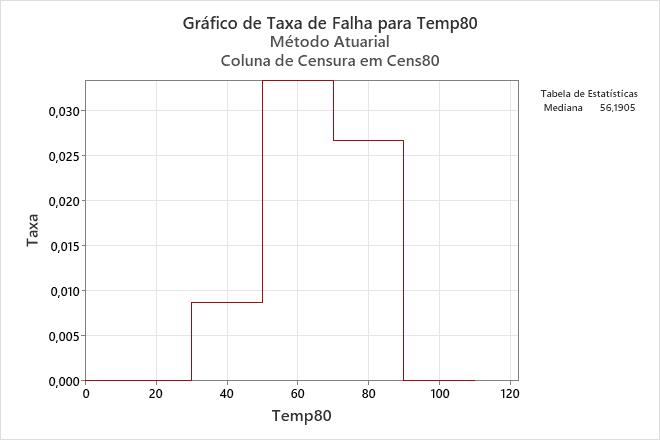
Interpretação
Para enrolamentos de motor em funcionamento a 80 °C, a função de risco aumenta até o intervalo de 50 a 70 horas, e depois diminui após 70 horas.
Gráfico de modo de múltiplas falhas – método de estimativa de atuarial
Para os dados de múltiplas falhas, o Minitab exibe gráficos para cada modo de falha.
- Use o gráfico de sobrevivência para avaliar a probabilidade de que o item sobreviva até um determinado momento. O gráfico de sobrevivência mostra a confiabilidade do produto ao longo do tempo.
- Use a função de risco para visualizar uma medida da probabilidade de falha como uma função do tempo que uma unidade tenha sobrevivido (a taxa de falha instantânea em um determinado momento, t). O gráfico de risco mostra a tendência da taxa de falha ao longo do tempo.
Saída do exemplo
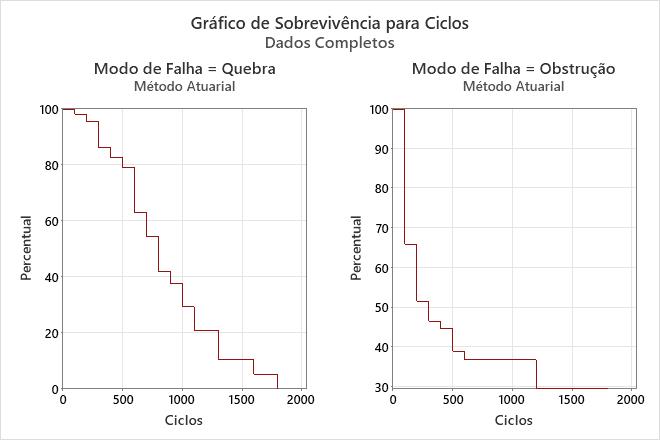
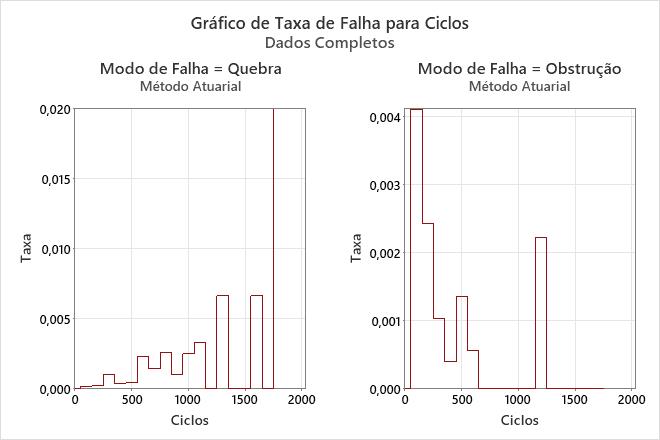
Interpretação
Para os dados de lava-louças, a probabilidade de que os braços de pulverização irão sobreviver a quebras durante 200 ciclos é de 95%, e que eles vão sobreviver a obstruções por 200 ciclos é de cerca de 51%.
A taxa de risco para quebras parece aumentar um pouco ao longo do tempo. No entanto, a taxa de risco de obstruções parece diminuir ao longo do tempo.
