Um engenheiro de confiabilidade estuda as taxas de falha de enrolamentos de motor de montagens de turbina para determinar o tempo no qual os enrolamentos falham. Em altas temperaturas, os enrolamentos podem se decompor muito rapidamente.
Os engenheiro registra os tempos de falha para os enrolamentos do motor a 80 °C e 100 °C. No entanto, algumas das unidades precisaram ser removidas do teste antes de falhar. Portanto, os dados são censurados à direita. O engenheiro usa Análise de Distribuição Não-paramétrica (censura à direita) para determinar o seguinte:
- Os tempos em que várias porcentagens dos enrolamentos falham.
- A porcentagem de enrolamentos que sobreviverá além dos vários tempos.
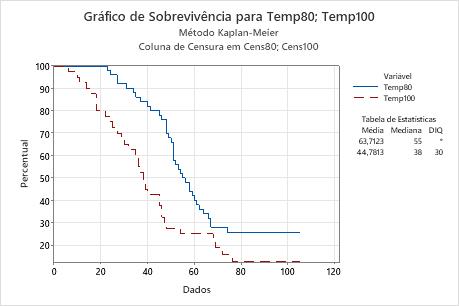
- A função de sobrevivência para os enrolamentos de motor (como mostrado em um gráfico de sobrevivência).
- Se as curvas de sobrevivência às duas temperaturas são significativamente diferentes.
- Abra os dados amostrais, ConfiabilidadeDoEnrolamentoDoMotor.MWX.
- Selecione .
- Em Variáveis, insira Temp80Temp100.
- Clique em Censura. Sob Usar colunas de censura, insira Cens80Cens100.
- Em Valor de censura, digite 0. Clique em OK.
- Clique em Gráficos. Selecione Gráfico de sobrevivência.
- Clique em OK em cada caixa de diálogo.
Interpretar os resultados
O tempo de falha mediano estimado para Temp80 é de 55 horas e o tempo de falha mediano estimado para Temp100 é de 38 horas. Portanto, o aumento da temperatura reduz o tempo de falha mediano em aproximadamente 17 horas.
O Minitab exibe as estimativas de sobrevivência na tabela Estimativas de Kaplan-Meier. A 80 °C, 0,9000 (90%) dos enrolamentos sobrevivem após 31 horas. A 100 °C, 0,9000 (90%) dos enrolamentos sobrevivem após 14 horas.
Na tabela Estatísticas de Teste, um valor-p < α (geralmente, α = 0,05) indica que as curvas de sobrevivência são significativamente diferentes. Neste caso, os dois valores-p (0,005 e 0,000) são menores do que α, o que sugere que uma mudança de 20 °C tem um efeito sobre a quebra dos enrolamentos do motor.
- 80° C
- Variável: Temp80
Censura
Informações de Censura Contagem Valor não-censurados 37 Valor censurado à direita 13 Estimativas Não-paramétricasCaracterísticas da Variável
IC Normal de 95,0% Média (TMPF) Erro Padrão Inferior Superior Q1 Mediana Q3 DIQ 63,7123 3,83453 56,1968 71,2279 48 55 * * Estimativas de Kaplan-Meier
Número
sob
RiscoNúmero
com
FalhaProbabilidade
de
SobrevivênciaIC Normal de 95,0% Tempo Erro Padrão Inferior Superior 23 50 1 0,980000 0,0197990 0,941195 1,00000 24 49 1 0,960000 0,0277128 0,905684 1,00000 27 48 2 0,920000 0,0383667 0,844803 0,99520 31 46 1 0,900000 0,0424264 0,816846 0,98315 34 45 1 0,880000 0,0459565 0,789927 0,97007 35 44 1 0,860000 0,0490714 0,763822 0,95618 37 43 1 0,840000 0,0518459 0,738384 0,94162 40 42 1 0,820000 0,0543323 0,713511 0,92649 41 41 1 0,800000 0,0565685 0,689128 0,91087 45 40 1 0,780000 0,0585833 0,665179 0,89482 46 39 1 0,760000 0,0603987 0,641621 0,87838 48 38 3 0,700000 0,0648074 0,572980 0,82702 49 35 1 0,680000 0,0659697 0,550702 0,80930 50 34 1 0,660000 0,0669925 0,528697 0,79130 51 33 4 0,580000 0,0697997 0,443195 0,71680 52 29 1 0,560000 0,0701997 0,422411 0,69759 53 28 1 0,540000 0,0704840 0,401854 0,67815 54 27 1 0,520000 0,0706541 0,381521 0,65848 55 26 1 0,500000 0,0707107 0,361410 0,63859 56 25 1 0,480000 0,0706541 0,341521 0,61848 58 24 2 0,440000 0,0701997 0,302411 0,57759 59 22 1 0,420000 0,0697997 0,283195 0,55680 60 21 1 0,400000 0,0692820 0,264210 0,53579 61 20 1 0,380000 0,0686440 0,245460 0,51454 62 19 1 0,360000 0,0678823 0,226953 0,49305 64 18 1 0,340000 0,0669925 0,208697 0,47130 66 17 1 0,320000 0,0659697 0,190702 0,44930 67 16 2 0,280000 0,0634980 0,155546 0,40445 74 13 1 0,258462 0,0621592 0,136632 0,38029 - 100° C
- Variável: Temp100
Censura
Informações de Censura Contagem Valor não-censurados 34 Valor censurado à direita 6 Estimativas Não-paramétricasCaracterísticas da Variável
IC Normal de 95,0% Média (TMPF) Erro Padrão Inferior Superior Q1 Mediana Q3 DIQ 44,7813 4,43366 36,0914 53,4711 24 38 54 30 Estimativas de Kaplan-Meier
Número
sob
RiscoNúmero
com
FalhaProbabilidade
de
SobrevivênciaIC Normal de 95,0% Tempo Erro Padrão Inferior Superior 6 40 1 0,97500 0,0246855 0,926617 1,00000 10 39 1 0,95000 0,0344601 0,882459 1,00000 11 38 1 0,92500 0,0416458 0,843376 1,00000 14 37 1 0,90000 0,0474342 0,807031 0,99297 16 36 1 0,87500 0,0522913 0,772511 0,97749 18 35 3 0,80000 0,0632456 0,676041 0,92396 22 32 1 0,77500 0,0660256 0,645592 0,90441 24 31 1 0,75000 0,0684653 0,615810 0,88419 25 30 1 0,72500 0,0706001 0,586626 0,86337 27 29 1 0,70000 0,0724569 0,557987 0,84201 29 28 1 0,67500 0,0740566 0,529852 0,82015 30 27 1 0,65000 0,0754155 0,502188 0,79781 32 26 1 0,62500 0,0765466 0,474972 0,77503 35 25 1 0,60000 0,0774597 0,448182 0,75182 36 24 2 0,55000 0,0786607 0,395828 0,70417 37 22 1 0,52500 0,0789581 0,370245 0,67975 38 21 2 0,47500 0,0789581 0,320245 0,62975 39 19 1 0,45000 0,0786607 0,295828 0,60417 40 18 1 0,42500 0,0781625 0,271804 0,57820 45 17 2 0,37500 0,0765466 0,224972 0,52503 46 15 2 0,32500 0,0740566 0,179852 0,47015 47 13 1 0,30000 0,0724569 0,157987 0,44201 48 12 1 0,27500 0,0706001 0,136626 0,41337 54 11 1 0,25000 0,0684653 0,115810 0,38419 68 8 1 0,21875 0,0666585 0,088102 0,34940 69 7 1 0,18750 0,0640434 0,061977 0,31302 72 6 1 0,15625 0,0605154 0,037642 0,27486 76 5 1 0,12500 0,0559017 0,015435 0,23457 - Comparação de Curvas de Sobrevivência
Estatísticas de Teste
Método Qui-Quadrado GL Valor-p Log-posto 7,7152 1 0,005 Wilcoxon 13,1326 1 0,000
