Neste tópico
Estimativa de Kaplan-Meier
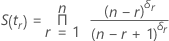
com S(t0) = 1 e t0 = 0.
Função de risco empírico
A função de risco descreve a taxa de falha para um intervalo. A função de risco é 0 antes da primeira observação censurada. A função de risco muda apenas com observações não censuradas. O Minitab não representa graficamente a função de risco após o último ponto de dados sem censura.

Quando existem empates, o Minitab usa a maior posto no empate para estimar a função de risco. Consulte Nelson1 para obter mais detalhes.
Tempo médio até a falha
Para dados sem censura, o tempo médio até a falha é igual ao tempo médio de falha. A fórmula geral a ser usada com dados censurados ou sem censura segue abaixo:
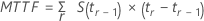
Além disso, quando a maior observação é censurada, o Minitab trata o tempo de maior observação sem censura como um limite de tempo para o cálculo. Consulte Lee2 para obter mais detalhes.
Erro padrão de MTTF
O erro padrão do tempo médio até a falha é a raiz quadrada da variância. Quando todas as observações são sem censura, o Minitab calcula uma estimativa não viciada:
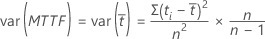
Para os casos em que alguns dados são censurados, a estimativa não viciada da variância é a fórmula a seguir:

Por causa da forma da função de risco empírico, as áreas sob a curva de sobrevivência, Ar, são retângulos com alturas iguais para a função de sobrevivência e comprimentos iguais aos intervalos entre as observações não censuradas.
Notação
| Termo | Descrição |
|---|---|
| tr | tempo do ponto de dados com posto r |
| r | posto do ponto de dados, onde a falha mais antiga tem o posto mais baixo |
| n | número total de unidades |
| δr | 0 se a ja observação for censurada ou 1 se a ja observação for sem censura |
| c | número de pontos de dados até a próxima observação sem censura |
| S(tr) | função de sobrevivência empírica no tempo tr |
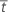 | estresse de falha média |
| Ar | área sob a curva do gráfico de sobrevivência à direita de tr |
| m | número total de observações sem censura |
Referências
1. W. Nelson (1982). Applied Life Data Analysis. John Wiley & Sons, Inc. 133.
2. Elisa T. Lee (1992). Statistical Methods for Survival Data Analysis, Second Edition. John Wiley & Sons, Inc. 73-76.
Estimativa atuarial
O modelo atuarial é uma análise não paramétrica alternativa que exibe informações para grupos de tempos de falha. O método de Kaplan-Meier assume que as suspensões em um intervalo ocorrem no final desse intervalo, depois que as falhas ocorreram. O modelo atuarial do Minitab assume que as suspensões ocorrem no meio do intervalo, que tem o efeito de reduzir o número de unidades disponíveis no intervalo. A estimativa da função de sobrevivência usando o método atuarial é da seguinte maneira:
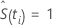 para i = 0
para i = 0
 Para i > 0
Para i > 0
Função de risco empírico
A função de risco descreve a taxa de falha para um intervalo. Com estimativa atuarial, você assume que o cálculo é para o ponto médio do intervalo. No gráfico de risco, a função é desenhada a partir de um ponto médio para outro. Para obter mais detalhes, consulte as referências a seguir na seção Notação.
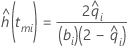
Notação
| Termo | Descrição |
|---|---|
| ni | o número de unidades a serem inseridas em um intervalo |
| di | o número de falhas no intervalo |
| n'i |  |
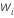 | o número censurado em um intervalo |
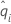 | a probabilidade condicional de um evento, que é igual a di/n'i |
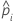 |  |
| tmi | tempo no ponto médio do intervalo atuarial |
| bi | o comprimento do intervalo atuarial |
Referências
Collett, D. (1994) Modelling Survival Data in Medical Research, Chapman and Hall.
Lee, Elisa T. (1992) Statistical Methods for Survival Data Analysis, 2nd Edition, John Wiley & Sons.
Estimativa de Turnbull
Turnbull1, 2 desenvolveu um algoritmo iterativo para calcular uma estimativa de máxima verossimilhança não paramétrica da função distribuição acumulada para os dados. Este método se aplica a situações mais gerais, por exemplo, em que os intervalos se sobrepõem.
O Minitab exibe a saída resumindo a estimativa de Turnbull das probabilidades de intervalo, juntamente com os erros padrão para estas probabilidades.
Referências
- B.W. Turnbull (1976). "The Empirical Distribution Function with Arbitrarily Grouped, Censored and Truncated Data," Journal of the Royal Statistical Society 38, pp. 290-295.
- B.W. Turnbull (1974). "Nonparametric Estimation of a Survivorship Function with Doubly Censored Data," Journal of the American Statistical Association 69, 345, pp. 169-173.
Intervalos de confiança
Independentemente do método de estimativa, o Minitab usa uma aproximação normal para calcular intervalos de confiança. Os intervalos de confiança são como a seguir:
Fórmula
Estimativa da probabilidade de sobrevivência  zα × Erro padrão da estimativa
zα × Erro padrão da estimativa
Notação
| Termo | Descrição |
|---|---|
| zα | o 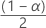 valor crítico superior para a distribuição normal padrão valor crítico superior para a distribuição normal padrão |
| α | o nível de confiança |
