Neste tópico
Estimativas de parâmetros
Fórmula
| Distribuição | Parâmetros |
|---|---|
|
Menor valor extremo Normal Logística |
μ = local, σ = escala, σ > 0 |
|
Lognormal Loglogística |
μ = local, μ > 0 σ = escala, σ > 0 |
|
Lognormal para 3 parâmetros Loglogística para 3 parâmetros |
μ = local, μ > 0 σ = escala, σ > 0 λ = limite. |
|
Weibull |
α = escala, α = exp(μ) β = forma, β = 1/σ |
|
Weibull com 3 parâmetros |
α = escala, α = exp(μ) β = forma, β = 1/σ λ = limite, |
|
Exponencial |
θ = escala, θ > 0 |
|
Exponencial com 2 parâmetros |
θ = escala, θ > 0 λ = limite, |
Erro padrão das estimativas de parâmetros
O erro padrão é o desvio padrão da estimativa do parâmetro. O erro padrão proporciona uma medida da variabilidade em cada estimativa.
, 
, 
, 
, 
e 
denota o erro padrão da MLE de μ, σ, α, β, θ e λ. Cada erro padrão é calculado como a raiz quadrada do elemento da diagonal correto da inversa da matriz de informação de Fisher.
Limites de confiança para estimativas de parâmetros
Fórmula
| Distribuição | Parâmetro | Limite inferior de confiança | Limite superior de confiança |
|---|---|---|---|
| Menor valor extremo, normal, logística, lognormal, loglogístico | Localização, μ |
 |
 |
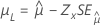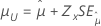| Escala, σ |
 |
 |
|
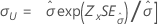| lognormal de 3 parâmetros, loglogístico de 3 parâmetros | Localização, μ |
 |
 |
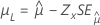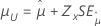| Escala, σ |
 |
 |
|
| Limite, λ |
 |
 |
|
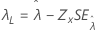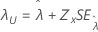| Weibull | Forma, β |
 |
 |
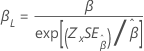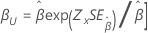| Escala, α |
 |
 |
|
|
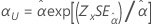Weibull com 3 parâmetros |
Forma, β |
 |
 |
|
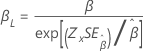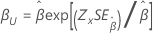Escala, α |
 |
 |
|
|
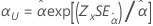Limite, λ |
 |
 |
|
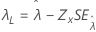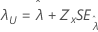| Exponencial | Escala |
 |
 |
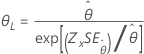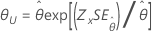| Exponencial com 2 parâmetros | Escala, θ |
 |
 |
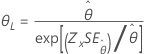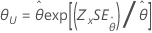| Limite, λ |
 |
 |
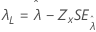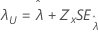Observação
Para alguns dos dados, a função de verossimilhança é ilimitada e, por conseguinte, produz estimativas inconsistentes para distribuições com um parâmetro de limite (como o exponencial de 2 parâmetros). Quando isso acontece, a matriz de variância-covariância dos parâmetros estimados não pode ser determinada numericamente. Neste caso, que o Minitab supõe que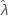 
é fixo, resultando em EP (
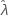) = 0. O limite superior e inferior para 
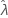é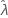 
.
Notação
| Termo | Descrição |
|---|---|
| zx | o 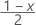 valor crítico superior para a distribuição normal padrão em que 100x % é o nível de confiança e 0 < x < 1. |
