Gráfico de probabilidade
- Os pontos do gráfico, que são os percentis estimados para corresponder às probabilidade de um conjunto de dados ordenado.
- A linha ajustada, que é o percentil esperado a partir da distribuição com base em estimativas de parâmetros de máxima verossimilhança.
- Os intervalos de confiança, que são os intervalos de confiança para os percentis.
Como os pontos do gráfico não dependem de qualquer distribuição, eles seriam os mesmos (antes da transformação) para qualquer gráfico de probabilidade criado. No entanto, a linha ajustada é diferente, dependendo da distribuição paramétrica escolhida. Assim, você pode usar o gráfico de probabilidade para determinar se uma distribuição específica se ajusta aos seus dados. Em geral, quanto mais próximos estiverem os pontos da linha ajustada, melhor o ajuste.
Pontos do gráfico
- Método do Rank Mediano (padrão)
- Método modificado de Kaplan-Meier
- Método de Herd-Johnson
- Método de Kaplan-Meier
Se os dados contiverem tempos de falha empatados (tempos de falha idênticos), todos os pontos (padrão), a média (mediana) ou o máximo dos pontos empatados são representados graficamente. Se o empate envolve falhas e suspensões, a ocorrência de falhas é considerada antes das suspensões.
Cada um desses métodos gera estimativas não paramétricas de F(t), a função distribuição acumulada para a variável aleatória T, que é o tempo até a falha.
Para uma amostra de n observações, sejam x(1), x(2),...,x(n) as estatísticas de ordem, ou os dados ordenados do menor ao maior. Então i é o posto da I a observação ordenada x(I). A fórmula para cada método é como a seguir:
Rank Mediano (método de Benard)
Fórmula para dados sem censura
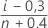
Fórmula para dados censurados

Modificado de Kaplan-Meier
Fórmula para dados sem censura
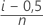
Fórmula para dados censurados
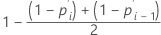
Estimativa de Herd-Johnson
Fórmula para dados sem censura

Fórmula para dados censurados
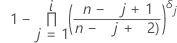
Estimativa de limite de produto de Kaplan-Meier
Observação
Se a maior observação é sem censura, o método de Kaplan-Meier resulta em p = 1 para a maior observação sem censura. Neste caso, a estimativa de Kaplan-Meier para a maior observação resulta em um número que não pode ser usado no gráfico. Este problema é corrigido pelo recálculo do maior p como 90% da distância entre o p anterior e 1.
Observação
Para dados com censura arbitrária, o Minitab estima as probabilidades acumuladas usando o método Turnbull1.
Fórmula para dados sem censura

Fórmula para dados censurados
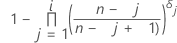
Notação
| Termo | Descrição |
|---|---|
| i | posto do ponto de dados, com empates dados em postos consecutivos |
| n | número de observações nos dados |
| δj | 0 se a j a observação é censurada, ou 1 se a j a observação é sem censura |
| ARi |
 |
| AR0 | é igual a 0 |
| p'i |
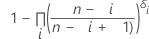 |
Linha ajustada
- O Minitab transforma o eixo-x para uma escala de log quando você está usando uma distribuição Weibull, Weibull de 3 parâmetros, exponencial, lognormal e loglogística.
- Por padrão, o Minitab transforma o eixo-y para uma escala percentual. Se você alterar o tipo de escala-y para probabilidade, o Minitab transforma o eixo-y para uma escala de probabilidade.
| Distribuição | coordenada x | coordenada y |
|---|---|---|
| Menor valor extremo | tempo de falha | ln(–ln(1 – p)) |
| Weibull | ln(tempo de falha) | ln(–ln(1 – p)) |
| Weibull com 3 parâmetros | ln(tempo de falha – limite) | ln(–ln(1 – p)) |
| Exponencial | ln(tempo de falha) | ln(–ln(1 – p)) |
| Exponencial com 2 parâmetros | ln(tempo de falha – limite) | ln(–ln(1 – p)) |
| Normal | tempo de falha | Φ –1 (p) |
| Lognormal | ln(tempo de falha) | Φ –1 (p) |
| Lognormal para 3 parâmetros | ln(tempo de falha – limite) | Φ –1 (p) |
| Logística | tempo de falha |
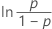 |
| Loglogística | ln(tempo de falha) |
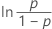 |
| Loglogística para 3 parâmetros | ln(tempo de falha – limite) |
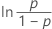 |
Notação
| Termo | Descrição |
|---|---|
| Φ –1 | fda inversa para a distribuição normal padrão |
| ln (x) | log natural de x |
