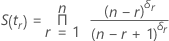
com S(t0) = 1 e t0 = 0.
Função de risco empírico
A função de risco descreve a taxa de falha para um intervalo. A função de risco é 0 antes da primeira observação censurada. A função de risco muda apenas com observações não censuradas. O Minitab não representa graficamente a função de risco após o último ponto de dados sem censura.

Quando existem empates, o Minitab usa a maior posto no empate para estimar a função de risco. Consulte Nelson1 para obter mais detalhes.
Tempo médio até a falha
Para dados sem censura, o tempo médio até a falha é igual ao tempo médio de falha. A fórmula geral a ser usada com dados censurados ou sem censura segue abaixo:
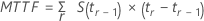
Além disso, quando a maior observação é censurada, o Minitab trata o tempo de maior observação sem censura como um limite de tempo para o cálculo. Consulte Lee2 para obter mais detalhes.
Erro padrão de MTTF
O erro padrão do tempo médio até a falha é a raiz quadrada da variância. Quando todas as observações são sem censura, o Minitab calcula uma estimativa não viciada:
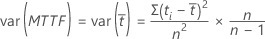
Para os casos em que alguns dados são censurados, a estimativa não viciada da variância é a fórmula a seguir:

Por causa da forma da função de risco empírico, as áreas sob a curva de sobrevivência, Ar, são retângulos com alturas iguais para a função de sobrevivência e comprimentos iguais aos intervalos entre as observações não censuradas.
Notação
| Termo | Descrição |
|---|---|
| tr | tempo do ponto de dados com posto r |
| r | posto do ponto de dados, onde a falha mais antiga tem o posto mais baixo |
| n | número total de unidades |
| δr | 0 se a ja observação for censurada ou 1 se a ja observação for sem censura |
| c | número de pontos de dados até a próxima observação sem censura |
| S(tr) | função de sobrevivência empírica no tempo tr |
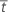 | estresse de falha média |
| Ar | área sob a curva do gráfico de sobrevivência à direita de tr |
| m | número total de observações sem censura |
Referências
1. W. Nelson (1982). Applied Life Data Analysis. John Wiley & Sons, Inc. 133.
2. Elisa T. Lee (1992). Statistical Methods for Survival Data Analysis, Second Edition. John Wiley & Sons, Inc. 73-76.
