Use o gráfico de probabilidade para comparar os ajustes das distribuições comuns a fim de escolher a distribuição de melhor ajuste. Se os pontos de dados caírem ao longo de uma linha reta no gráfico de probabilidade, é possível concluir que é razoável modelar os dados usando essa distribuição. Portanto, a distribuição de melhor ajuste é aquela em que os pontos seguem mais de perto a linha ajustada.
Os pontos do gráfico são os percentis estimados para as falhas com base em um método não paramétrico. Quando o ponteiro do mouse é mantido sobre um ponto de dados, o Minitab exibe o tempo de falha observado e a probabilidade acumulada estimada.
A linha está baseada na distribuição ajustada. Neste exemplo, Weibull, lognormal, exponencial e normal são distribuições ajustadas. Quando o ponteiro do mouse é mantido sobre a linha ajustada, o Minitab exibe uma tabela de percentis para várias porcentagens.
Para o método de máxima verossimilhança (MLE), o Minitab exibe a estatística de Anderson-Darling (ajust) para avaliar o ajuste de cada distribuição.
Quando você usa o método de estimativa dos mínimos quadrados (LSXY), o Minitab exibe o coeficiente de correlação de Pearson, que é um número positivo que não pode ser maior que 1. Os valores de coeficiente de correlação mais elevados indicam que a distribuição proporciona um melhor ajuste aos dados.
Observação
Para obter mais informações sobre como interpretar a estatística de Anderson-Darling (ajust), acesse "Qualidade do ajuste".
Saída do exemplo
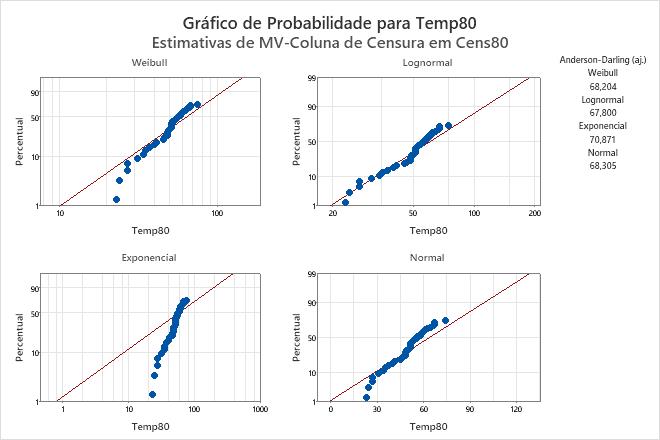
Interpretação
Para os dados dos enrolamentos do motor, os gráficos de probabilidade mostram que a distribuição Weibull e a distribuição lognormal ajustam os dados muito melhor do que a distribuição exponencial ou a distribuição normal. A distribuição lognormal parece ajustar melhor estes dados.
