Um engenheiro de confiabilidade quer avaliar a confiabilidade de um novo tipo de silenciador e calcular a taxa de reclamações de garantia que poderá ser esperada com uma garantia de 50.000 milhas. O engenheiro coleta dados de falha no tipo antigo e no novo tipo de silenciador. Os silenciadores foram inspecionados quanto a falhas a cada 10.000 milhas.
O engenheiro registra o número de falhas para cada intervalo de 10.000 milhas. Portanto, os dados são arbitrariamente censurados. Antes de analisar os dados de falha para os novos silenciadores usando Análise de Distribuição Paramétrica (Censura Arbitrária), o engenheiro usa um gráfico ID de distribuição (Censura Arbitrária) para selecionar um modelo de distribuição para a análise.
- Abra os dados das amostras, ConfiabilidadeSilencioso.MWX.
- Selecione .
- Em Variáveis iniciais, insira InícioNovo.
- Em Variáveis finais, insira FimNovo.
- Em Colunas de frequência (opcional), insira FreqNovo.
- Selecione Especificar. Certifique-se de que as distribuições padrão sejam selecionadas (Weibull, Lognormal, Exponencial e Normal).
- Clique em OK.
Interpretar os resultados
No gráfico de probabilidade de Weibull, os pontos caem aproximadamente na linha reta. Portanto, a distribuição Weibull fornece um bom ajuste. O engenheiro decide, dessa maneira, usar a distribuição Weibull para modelar os dados para a Análise de Distribuição Paramétrica (Censura Arbitrária).
O Minitab também exibe uma tabela de percentis e uma tabela de tempo médio até a falha (MTTF), que fornecem tempos de falha calculados para cada distribuição. É possível comparar os valores calculados para saber como suas conclusões podem mudar com diferentes distribuições. Se várias distribuições oferecem bom ajuste aos seus dados, talvez seja desejável usar a distribuição que fornece os resultados mais conservadores.
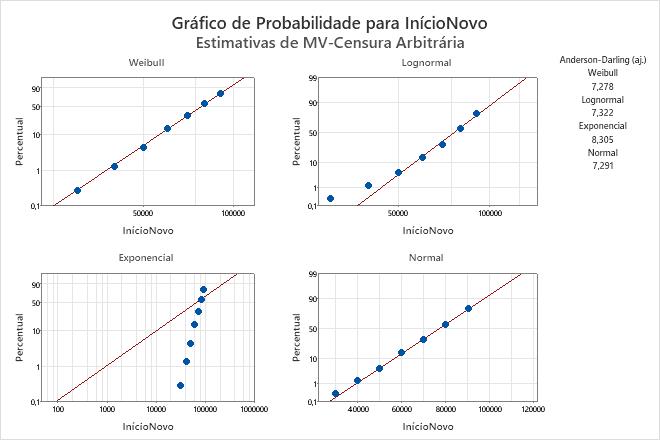
Teste de Qualidade de Ajuste
| Distribuição | Anderson-Darling (aj.) |
|---|---|
| Weibull | 7,278 |
| Lognormal | 7,322 |
| Exponencial | 8,305 |
| Normal | 7,291 |
Tabela de Percentis
| IC Normal de 95% | |||||
|---|---|---|---|---|---|
| Distribuição | Percentual | Percentil | Erro Padrão | Inferior | Superior |
| Weibull | 1 | 37265,1 | 938,485 | 35470,3 | 39150,6 |
| Lognormal | 1 | 43817,7 | 688,033 | 42489,7 | 45187,2 |
| Exponencial | 1 | 941,789 | 32,5296 | 880,143 | 1007,75 |
| Normal | 1 | 39810,3 | 1047,34 | 37757,6 | 41863,1 |
| Weibull | 5 | 49434,9 | 841,147 | 47813,5 | 51111,3 |
| Lognormal | 5 | 51458,9 | 624,451 | 50249,5 | 52697,5 |
| Exponencial | 5 | 4806,55 | 166,019 | 4491,93 | 5143,21 |
| Normal | 5 | 50694,9 | 810,524 | 49106,3 | 52283,5 |
| Weibull | 10 | 56006,1 | 759,186 | 54537,7 | 57514,0 |
| Lognormal | 10 | 56063,1 | 585,905 | 54926,4 | 57223,3 |
| Exponencial | 10 | 9873,05 | 341,017 | 9226,79 | 10564,6 |
| Normal | 10 | 56497,5 | 699,183 | 55127,1 | 57867,8 |
| Weibull | 50 | 77639,9 | 501,312 | 76663,5 | 78628,7 |
| Lognormal | 50 | 75850,3 | 576,625 | 74728,5 | 76988,9 |
| Exponencial | 50 | 64952,9 | 2243,49 | 60701,3 | 69502,3 |
| Normal | 50 | 76966,0 | 514,756 | 75957,1 | 77974,9 |
Tabela de MTTF
| IC Normal de 95% | ||||
|---|---|---|---|---|
| Distribuição | Média | Erro Padrão | Inferior | Superior |
| Weibull | 76585,0 | 488,71 | 75633,1 | 77549 |
| Lognormal | 77989,9 | 615,96 | 76792,0 | 79207 |
| Exponencial | 93707,3 | 3236,67 | 87573,5 | 100271 |
| Normal | 76966,0 | 514,76 | 75957,1 | 77975 |
