Confiabilidade é proporcionada
Se você especificar a meta de confiabilidade em termos um tempo e uma confiabilidade, o Minitab calcula em primeiro lugar o parâmetro a ser demonstrado utilizando a fórmula para a distribuição especificada na tabela a seguir.
Em seguida, o Minitab calcula o tempo de teste ou do tamanho amostral da mesma maneira como no caso de testes comprovação.
| Distribuição (parâmetro) | Parâmetro a ser demonstrado |
|---|---|
| Weibull (escala) |
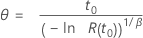 |
| Exponencial (média) |
 |
|
Menor valor extremo (local) Normal (média) Logística (média) |
 |
|
Lognormal (log-local) Loglogística (log-local) |
 |
Notação
| Termo | Descrição |
|---|---|
| t | tempo |
| R(t) | função de confiabilidade |
| θ | escala (Weibull) ou média (exponencial) |
| β | parâmetro de forma (Weibull) |
| σ | parâmetro de escala (lognormal, loglogística, logística, normal, menor valor extremo) |
| μ | média (normal, logística) ou log-local (lognormal, loglogística) |
| Φ-1 | FDA inversa para a distribuição correspondente |
Pº percentil é fornecido
Se você especificar a meta de confiabilidade em termos do Po percentil (tp), o Minitab calcula em primeiro lugar o parâmetro a ser demonstrado utilizando a fórmula para a distribuição especificada na tabela a seguir.
Em seguida, o Minitab calcula o tempo de teste ou do tamanho amostral da mesma maneira como no caso de testes comprovação.
| Distribuição (parâmetro) | Parâmetro a ser demonstrado |
|---|---|
| Weibull (escala) |
 |
| Exponencial (média) |
 |
|
Menor valor extremo (local) Normal (média) Logística (média) |
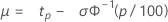 |
|
Lognormal (log-local) Loglogística (log-local) |
 |
Notação
| Termo | Descrição |
|---|---|
| t | tempo |
| R(t) | função de confiabilidade |
| p | percentil |
| α | escala (Weibull) |
| θ | média (exponencial) |
| μ | média (normal, logística), local (menor valor extremo) ou log-local (lognormal, loglogística) |
| Φ-1 | FDA inversa para a distribuição correspondente |
MTTF é fornecido
Se você especificar a meta de confiabilidade em termos do MTTF, o Minitab calcula em primeiro lugar o parâmetro a ser demonstrado utilizando a fórmula para a distribuição especificada na tabela a seguir.
Em seguida, o Minitab calcula o tempo de teste ou do tamanho amostral da mesma maneira como no caso de testes comprovação.
| Distribuição (parâmetro) | Parâmetro a ser demonstrado |
|---|---|
| Weibull (escala) |
 |
| Exponencial (média) |
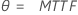 |
|
Normal (média) Logística (média) |
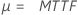 |
|
Lognormal (log-local) |
 |
|
Loglogística (log-local) |
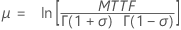 |
|
Menor valor extremo (local) |
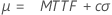 |
Notação
| Termo | Descrição |
|---|---|
| α | escala (Weibull) |
| σ | escala (lognormal, loglogística, distribuição de menor valor extremo) |
| β | forma (Weibull) |
| θ | média (exponencial) |
| μ | média (normal, logística), local (menor valor extremo) ou log-local (lognormal, loglogística) |
| MTTF | tempo médio até a falha |
| c | constante de Euler ≈ 0,5772 |
| Γ | função gama |
