Funções de confiabilidade e de confiabilidade inversa
Menor valor extremo
- Confiabilidade
-

- Confiabilidade inversa
-

onde
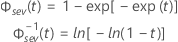
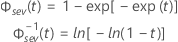
| Termo | Descrição |
|---|---|
| t | tempo |
| μ | parâmetro de localização |
| σ | parâmetro de escala |
| Φsev(t) | FDA da distribuição do menor valor extremo |
| Φ-1sev(t) | FDA inversa da distribuição do menor valor extremo |
Weibull
- Confiabilidade
-
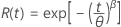
- Confiabilidade inversa
-

| Termo | Descrição |
|---|---|
| t | tempo |
| p | probabilidade probabilidade |
| β | parâmetro de forma |
| θ | parâmetro de escala |
Exponencial
- Confiabilidade
-

- Confiabilidade inversa
-
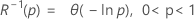
| Termo | Descrição |
|---|---|
| t | tempo |
| p | probabilidade probabilidade |
| θ | parâmetro de média |
Normal
- Confiabilidade
-
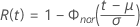
- Confiabilidade inversa
-

| Termo | Descrição |
|---|---|
| t | tempo |
| μ | parâmetro de localização |
| σ | parâmetro de escala |
| Φnor(t) | FDA da distribuição normal |
| Φ-1nor(t) | FDA inversa da distribuição normal |
Lognormal
- Confiabilidade
-

- Confiabilidade inversa
-
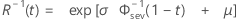
| Termo | Descrição |
|---|---|
| t | tempo |
| μ | parâmetro de localização |
| σ | parâmetro de escala |
| Φnor(t) | FDA da distribuição normal |
| Φ-1nor(t) | FDA inversa da distribuição normal |
Logística
- Confiabilidade
-
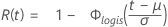
- Confiabilidade inversa
-
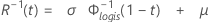
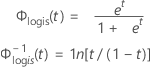
| Termo | Descrição |
|---|---|
| t | tempo |
| μ | parâmetro de localização |
| σ | parâmetro de escala |
| Φlogis(t) | FDA da distribuição logística |
| Φ-1logis(t) | FDA inversa da distribuição logística |
Loglogística
- Confiabilidade
-

- Confiabilidade inversa
-
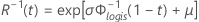
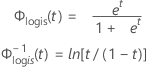
| Termo | Descrição |
|---|---|
| t | tempo |
| μ | parâmetro de localização |
| σ | parâmetro de escala |
| Φlogis(t) | FDA da distribuição logística |
| Φ-1logis(t) | FDA inversa da distribuição logística |
Equação
A equação para um plano de teste de m falhas é a seguinte:

Notação
| Termo | Descrição |
|---|---|
| α | alfa (o que equivale a 1 - o nível de confiança) |
| R | confiabilidade e função de sobrevivência no tempo t |
| N | número mínimo de unidades a serem testadas |
