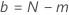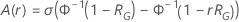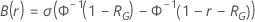Os cálculos para a probabilidade de passar um plano de teste dependem da distribuição que modela as falhas. Para uma distribuição em escala de loglocalização, a probabilidade é uma função da razão de melhoria. Para uma distribuição em escala de localização, a probabilidade é uma função da quantidade de melhoria. A expressão das fórmulas se divide perfeitamente em dois casos que dependerão do fato de você especifica o tamanho da amostra ou o tempo de teste.
Tamanho amostral
nível de
confiança satisfaz a seguinte equação: 
,
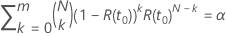
a solução, 
,
da equação tem a seguinte forma: 
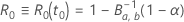
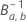é a função de distribuição acumulada inversa da distribuição beta com os
seguintes parâmetros de forma:
,
inverta a função 
.
A inversão depende da família de distribuição.
- Família em escala de loglocalização
- Família em escala de localização
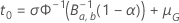
e a melhoria: 
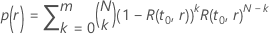
em que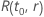 
é
a função de confiabilidade do modelo de distribuição em termos de
e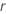 
.
- Família em escala de loglocalização
- Família em escala de localização
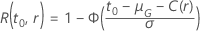
A tabela a seguir mostra a função de 
para a família de distribuição e o objetivo do teste:
| Meta de confiabilidade | ||||
|---|---|---|---|---|
|
|
|
|
|
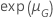
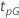
| Escala de loglocalização |    |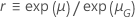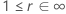
   |
   |
   |
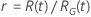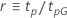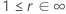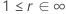| Meta de confiabilidade | ||||
|
|
|
|
|
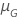
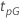
| Escala de localização |    |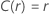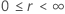
   |
   |
   |
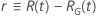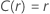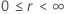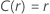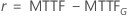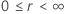Exemplo de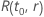 
para a distribuição Weibull
,
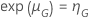e um determinado tamanho amostral, a probabilidade de passar tem a seguinte
forma: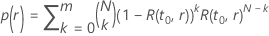 
em que
Tempo de teste
nível de
confiança satisfaz a seguinte equação: 
), a solução
da equação, 
,
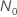tem a seguinte forma: 
), não existe
uma solução de forma fechada. Meeker e Escobar (1998)1 dá a seguinte solução aproximada: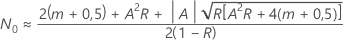 
em que
O Minitab encontra a solução numericamente exata quando 
.
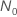e a melhoria: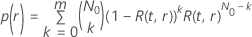 
em que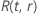 
é
a função de confiabilidade do modelo de distribuição em termos de
e
.
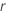- Família em escala de loglocalização
- Família em escala de localização
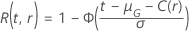
A função 
tem as mesmas definições às das condições em que as especificações do teste dão
o tamanho da amostra.
Exemplo de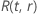 
para a distribuição Weibull
,
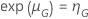e um determinado tempo de teste, a probabilidade de passar tem a seguinte
forma: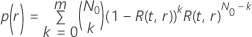 
em que
Notação
| Termo | Descrição |
|---|---|
| N | tamanho amostral para o experimento quando as especificações para o teste fornecem o tamanho amostral |
| m | número de unidades que falham durante o teste |
 | nível de significância, de tal forma que o nível de confiança para o teste
de demonstração é  |
 | parâmetro da escala |
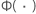 | função distribuição acumulada da distribuição padrão para a distribuição selecionada em escala de loglocalização ou escala de localização |
 | função de distribuição acumulada inversa da distribuição padrão para a distribuição selecionada em escala de loglocalização ou escala de localização |
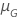 | parâmetro de localização para a distribuição que atende ao objetivo do teste |
 | parâmetro de forma da distribuição Weibull |
 | tempo de teste quando as especificações para o teste fornecem o tamanho amostral |
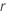 | razão de melhoria para distribuições em escala de loglocalização ou a quantidade de melhoria para distribuições em escala de localização |
 | confiabilidade no tempo t, que é o objetivo para o teste |
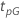 | percentil em p da porcentagem que é o objetivo para o teste |
 | tempo médio até a falha que é o objetivo do teste |
 | tempo de teste quando as especificações para o teste oferecem o tempo de teste |
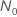 | tamanho amostral quando a especificação para o teste oferecer o tempo de teste |
