Métodos e fórmulas para as distribuições em Ajuste Modelo de Cox com Preditores Fixos apenas

A função de sobrevivência usa as seguintes definições:

Termo	Descrição
	os tempos distintos, ordenados, de eventos
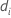	O número de eventos entre o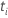
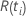	o risco definido no momento 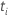, que é o conjunto de todas as unidades amostrais que ainda não falharam antes do tempo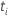
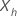	o vetor p-componente de valores covariados que representa um novo ou um ponto de dados existente

Dado: 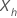, a função de sobrevivência do modelo de riscos proporcionais cox tem a seguinte forma:

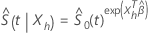
em que

e

A função 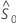estima a função de sobrevivência de um indivíduo quando os valores de todos os covariados são 0. A função é o estimador breslow da taxa de risco cumulativo da linha de base. A função é uma função de passo que salta nos tempos de evento observados.

Sob condições leves de regularidade, o estimador 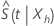tem uma distribuição normal assintótica com média e variância assintomática com a seguinte forma:

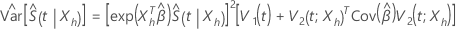
em que

e

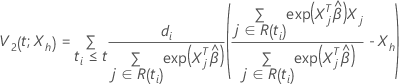
Um intervalo de confiança do método Wald direto está disponível, mas é menos preciso porque a distribuição de 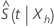é severamente distorcido. Além disso, os limites de confiança desses intervalos muitas vezes estão fora do intervalo [0, 1]. A distribuição do logaritmo de 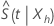é menos distorcido e converge mais rapidamente para a distribuição normal. Minitab faz uso das seguintes transformações para calcular os intervalos de confiança.

Transformação de log

Minitab calcula um intervalo de confiança para e volta a transformar os limites de confiança para fornecer o intervalo de confiança para 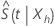. Usando esta abordagem, um intervalo de confiança aproximado de 100(1 – α) para 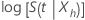, tem a seguinte forma:

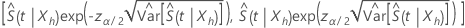
em que estima a variância assintomática de , tem a seguinte forma:

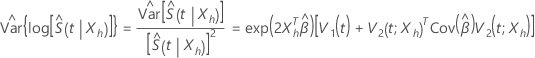
Colocar limite de confiança para 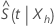excede 1, então Minitab usa 1 como limite superior.

Transformação do log natural

A transformação log-log garante que o intervalo de confiança para 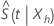Especificar constantes no intervalo (0@,1). Minitab calcula um intervalo de confiança para e volta a transformar os limites de confiança para fornecer o intervalo de confiança para 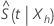. Usando este método, um intervalo de confiança aproximado de 100(1 – α) para , tem a seguinte forma:

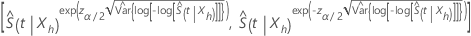
em que 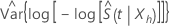estima a variância assintomática de , tem a seguinte forma: