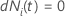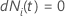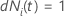| Termo | Descrição |
|---|---|
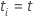
 | os tempos distintos, ordenados, de eventos |
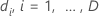 | O
número de eventos entre o 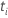 |
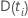 | o conjunto de todas as unidades que vivenciam o evento no momento
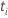 |
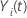 | uma variável indicadora que tem o valor 1 se sujeito
i está em risco no momento
t e 0 de outra forma, o que é equivalente a 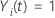 Se Se
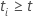 e e
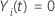 Senão
Senão |
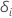 | um indicador para se o assunto
eu é censurado, de tal forma que 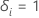 se o assunto
que eu experimentei o evento e se o assunto
que eu experimentei o evento e 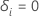 Senão
Senão |
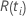 | o risco definido no momento 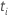 ,
que é o conjunto de todas as unidades amostrais que ainda não falharam antes do
tempo ,
que é o conjunto de todas as unidades amostrais que ainda não falharam antes do
tempo 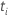 |
 | o número de eventos para sujeito i até e incluindo tempo t |
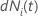 | a mudança em  para o assunto
i no momento
t tal que
para o assunto
i no momento
t tal que
|
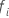 | o primeiro tempo de evento em que o assunto eu está no conjunto de risco |
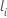 | o último tempo de evento em que o assunto eu está no conjunto de risco |
Resíduos de Cox-Snell
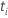 ,
tem a seguinte forma:
,
tem a seguinte forma: 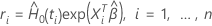
em que  é
o estimador do Breslow da taxa de risco cumulativo da linha de base:
é
o estimador do Breslow da taxa de risco cumulativo da linha de base:

 é
uma função passo com saltos nos horários observados. O valor do modelo no tempo
= 0.
é
uma função passo com saltos nos horários observados. O valor do modelo no tempo
= 0. 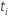 ,
tem a seguinte forma:
,
tem a seguinte forma: 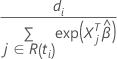

Para a aproximação de Efron, o residual de Cox-Snell tem a seguinte forma:
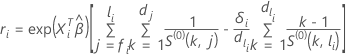
em que 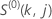 ,
tem a seguinte forma:
,
tem a seguinte forma:
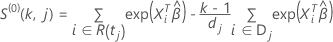
Para 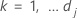
em que 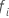 é o primeiro momento de evento em que o assunto
eu está no conjunto de risco e
é o primeiro momento de evento em que o assunto
eu está no conjunto de risco e 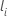 é o último momento de evento em que o assunto
i está no conjunto de risco.
é o último momento de evento em que o assunto
i está no conjunto de risco.
Resíduos de Martingale

em que 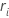 é o resíduo de Cox-Snell e depende do método de manuseio de gravatas. Aditivo
é o resíduo de Cox-Snell e depende do método de manuseio de gravatas. Aditivo
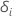 é um indicador para se o assunto
que eu sou censurado, de tal forma que
é um indicador para se o assunto
que eu sou censurado, de tal forma que 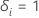 se o assunto
que eu experimentei o evento e
se o assunto
que eu experimentei o evento e 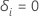 Senão
Senão
Resíduos deviance

em que  é o resíduo martingale para o assunto
i.
é o resíduo martingale para o assunto
i.
Vetor residual de Schoenfeld
O vetor residual de Schoenfeld é um vetor p-componente. Para o assunto i com tempo de evento t o vetor residual de Schoenfeld tem a seguinte forma:
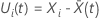
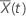 é
a média ponderada dos covariados sobre o conjunto de risco em tempo t. A média
ponderada tem a seguinte forma:
é
a média ponderada dos covariados sobre o conjunto de risco em tempo t. A média
ponderada tem a seguinte forma: 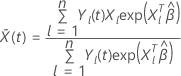
em que 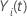 é
uma variável indicadora que tem o valor 1 se sujeito
i estiver em risco no momento
t e 0 de outra forma, o que equivale a
é
uma variável indicadora que tem o valor 1 se sujeito
i estiver em risco no momento
t e 0 de outra forma, o que equivale a 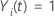 Se
Se
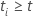 e
e
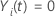 Senão
Senão
Se o sujeito não experimentar o evento no momento t,o vetor contém valores faltantes.
O cálculo do vetor residual de Schoenfeld depende do método de manuseio de gravatas. Para a aproximação de Breslow, o vetor residual de Schoenfeld tem a seguinte forma:
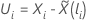
em que
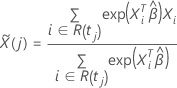
Para a aproximação de Efron, o vetor residual de Schoenfeld tem a seguinte forma:
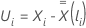
em que
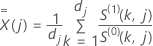
A função 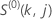 tem a definição igual à usada no caso de limite de especificação único.
tem a definição igual à usada no caso de limite de especificação único.
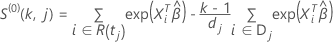
e
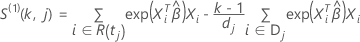
Para 
Vetor residual de Schoenfeld escalado
O vetor residual de Schoenfeld dimensionado tem a seguinte forma:

em que  é o número
observado de tempos de sobrevivência sem censura e
é o número
observado de tempos de sobrevivência sem censura e 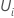 é o vetor residual de Schoenfeld.
é o vetor residual de Schoenfeld.
Vetor residual de pontuação
O cálculo do vetor residual de pontuação depende do método de aproximação para empates nos tempos de evento. Para a aproximação de Breslow, o vetor residual de pontuação tem a seguinte forma:
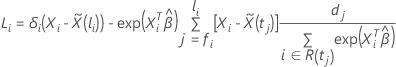
em que
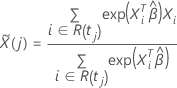
Para a aproximação de Efron, o vetor residual de escore tem a seguinte forma:
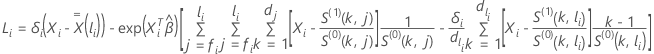
em que 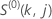 ,
,
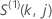 e
e
 têm as mesmas definições do vetor residual de Schoenfeld:
têm as mesmas definições do vetor residual de Schoenfeld:
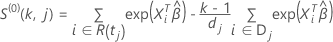
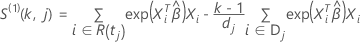
e
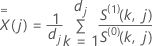
Para 
DFBeta
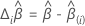

em que 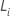 é o vetor residual de pontuação. Para obter mais detalhes sobre limites, vá
para
é o vetor residual de pontuação. Para obter mais detalhes sobre limites, vá
para  Ir Para
Métodos e fórmulas para os coeficientes e equação de regressão para Ajuste Modelo de Cox com Preditores Fixos apenas.
Ir Para
Métodos e fórmulas para os coeficientes e equação de regressão para Ajuste Modelo de Cox com Preditores Fixos apenas.