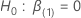Neste tópico
A análise da variância fornece um teste da significância estatística para cada preditor no modelo.
GL
A interpretação da razão de chances depende se a preditora é categórica ou contínua. Para um preditor categórico, os graus de liberdade são 1 menor do que o número de níveis, k, no preditor (k – 1). Para um preditor contínuo, os graus de liberdade são sempre 1. Para um termo de ordem superior, os graus de liberdade são o produto dos graus de liberdade nos termos compostos. Por exemplo, os graus de liberdade para a interação entre dois preditores categóricos de 3 níveis são 2 × 2 = 4.
Qui-quadrado
- Teste de Wald
- Teste da razão de verossimilhança
- Testes de pontuação
Se os clusters estiverem presentes no projeto, o Minitab fornece a tabela ANOVA com base no teste de Wald, porque a razão de probabilidade e os métodos de pontuação assumem que as observações dentro dos clusters são independentes.
Quando a variável de resposta não tem tempos de resposta empatados, o teste de pontuação é idêntico ao conhecido teste de classificação de log.
Definições:
Os cálculos para todos os 3 tipos de testes utilizam as seguintes definições.
Seja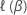 
ser a função de semelhança parcial de Breslow ou a função de probabilidade parcial Efron avaliada em β.
Seja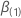 
ser um vetor q-componente e 
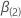ser um (p – q) -vetor de componentes para que os vetores de coeficiente de 2 p componentes tenham as seguintes definições: 
e 
.
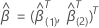Seja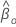 
ser a probabilidade máxima (parcial) de 
sob o modelo restrito onde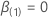 
. Em seguida, a estimativa de probabilidade máxima sob a hipótese nula tem a seguinte forma:
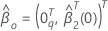
em que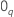 
é um vetor q-componente de zeros e 
é a probabilidade máxima (parcial) de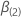 
Quando 
.
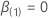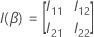
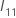é a seguinte matriz q × q:
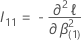
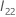é o seguinte p – q × p – q matriz:
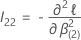
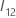e 
tem a seguinte definição:
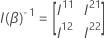
Sob a hipótese nula, a estatística de teste para cada um dos três testes (Wald, razão de probabilidade e testes de pontuação) tem uma distribuição assintomática do qui-quadrado com q graus de liberdade. A distribuição assintotótica é válida quando o número de eventos observados é grande em comparação com o número de parâmetros no modelo. Para preditores categóricos, o número de eventos em cada nível também deve ser grande o suficiente.
Teste de Wald
Para o teste de Wald, a estatística do teste tem a seguinte forma:
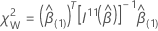
em que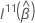 
é o superior q × q submatrix de 
.
Se o design tiver clusters, os cálculos fazem uso da robusta variância de Lin & Wei (1989)1. Seja 
ser a matriz de resíduos de pontuação. A matriz de variância-covariância tem a seguinte forma:
em qu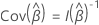e 
e 
é a matriz residual de pontuação colapsada. Para obter a matriz residual de escore colapsada, substitua cada conjunto de linhas residuais de escore pela soma dessas linhas residuais.
Teste da razão de verossimilhança
Para o teste da razão de verossimilhança, as hipóteses são as seguintes:
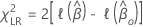
em que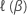 
é a função de padrão parcial de log apropriado.
Se os clusters estiverem presentes no projeto, o Minitab fornece a tabela ANOVA com base no teste de Wald, porque a razão de probabilidade e os métodos de pontuação assumem que as observações dentro dos clusters são independentes.
Testes de pontuação
Seja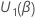 
ser o vetor de derivativos parciais da função log-probabilidade em relação a 
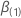. Especificamente, este vetor q-componente tem a seguinte forma:
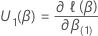
Em seguida, a estatística de teste para o teste de pontuação tem o seguinte formulário:
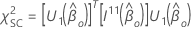
Se os clusters estiverem presentes no projeto, o Minitab fornece a tabela ANOVA com base no teste de Wald, porque a razão de probabilidade e os métodos de pontuação assumem que as observações dentro dos clusters são independentes.
Valor-p
O valor-p ajustado tem a seguinte expressão:
em que 
é uma variável aleatória que segue uma distribuição qui-quadrado com 
graus de liberdade. 
A estatística de teste
