Neste tópico
Passo 1: Determine se o modelo ajusta bem os dados
- Valor-p ≤ α: O modelo ajusta razoavelmente bens os dados.
- Se o valor-p for menor ou igual ao nível de significância, é possível concluir que a diferença entre os modelos é estatisticamente significativa. Você deve examinar se algum dos termos são estatisticamente significativos e também garantir que o modelo satisfaça a suposição de riscos proporcionais.
- Valor-p > α: Não há evidências suficientes para concluir que o efeito é estatisticamente significativo.
- Se o valor p for maior ou igual ao nível de significância, não é possível concluis que o modelo explica a variação na resposta. Talvez seja necessário reajustar o modelo sem o termo.
Testes de Qualidade de Ajuste
| Teste | GL | Qui-Quadrado | Valor-P |
|---|---|---|---|
| Razão de verossimilhança | 4 | 18,31 | 0,001 |
| Wald | 4 | 21,15 | 0,000 |
| Escore | 4 | 24,78 | 0,000 |
Principais resultados: Valor-P
Nesses resultados, os valores p para todos os 3 testes estão abaixo de 0,05, então você pode concluir que o modelo se encaixa bem nos dados.
Passo 2: Determinar se a associação entre a resposta e o termo é estatisticamente significativa
- Valor-p ≤ α: A associação é estatisticamente significativa
- Se o valor-p for menor ou igual ao nível de significância, é possível concluir que há uma associação estatisticamente significativa entre a variável resposta e o termo.
- Valor-p > α: a associação não é estatisticamente significativa
- Se o valor-p for maior ou igual ao nível de significância, não é possível concluir que há uma associação estatisticamente significativa entre a variável resposta e o termo. Talvez seja necessário reajustar o modelo sem o termo.
- Se um fator aleatório é significativo, é possível concluir que o fator contribui para a quantidade de variação na resposta.
- Se uma covariável for estatisticamente significativa, é possível concluir que as mudanças no valor da covariável estejam associadas a mudanças no valor médio da resposta.
- Se um termo de interação é significativo, a relação entre um fator e a resposta depende dos outros fatores do termo. Neste caso, você não deve interpretar os principais efeitos sem considerar o efeito da interação.
- Se um termo polinomial for significativo, é possível concluir que os dados contêm curvatura.
Análise de Variância
| Teste de Wald | |||
|---|---|---|---|
| Fonte | GL | Qui-Quadrado | Valor-P |
| Idade | 1 | 1,78 | 0,182 |
| Palco | 3 | 17,92 | 0,000 |
Principais resultados: Valor-P
Nestes resultados, o valor p para o estágio é significativo a um nível α de 0,05. Portanto, pode-se concluir que o estágio do câncer tem um efeito estatisticamente significativo na sobrevivência do paciente. No entanto, o valor p para a idade é de 0,182, portanto o efeito da idade não é significativo em um nível de α de 0,05.
Passo 3: Determinar os riscos relativos dos preditores
- Variável categórica
-
Na tabela Riscos Relativos para Preditores Categóricos, a Minitab rotula dois níveis da variável categórica como Nível A e Nível B. O risco relativo descreve a taxa de ocorrência do evento para o nível A em relação ao nível B. Por exemplo, nos resultados a seguir, o risco de vivenciar o evento para pacientes no estágio IV é 5,5 vezes maior do que o risco para pacientes no Estágio I.
- Variável contínua
- Na tabela Riscos Relativos para Preditores Contínuos, o Minitab exibe a unidade de alteração e o risco relativo. O risco relativo descreve a alteração na taxa de risco para cada unidade de alteração no valor do preditor. Por exemplo, nos seguintes resultados, um paciente tem 1,02 vezes mais chances de experimentar o evento para cada aumento de 1 ano até a idade.
Você pode usar o intervalo de confiança para determinar se o risco relativo é estatisticamente significativo. Normalmente, se o intervalo de confiança contiver 1, você não pode concluir que o risco relativo é estatisticamente significativo.
Riscos relativos para preditores contínuos
| Unidade de Mudança | Risco relativo | IC de 95% | |
|---|---|---|---|
| Idade | 1 | 1,0192 | (0,9911; 1,0481) |
Riscos relativos para preditores categóricos
| Nível A | Nível B | Risco relativo | IC de 95% |
|---|---|---|---|
| Palco | |||
| II | I | 1,1503 | (0,4647; 2,8477) |
| III | I | 1,9010 | (0,9459; 3,8204) |
| IV | I | 5,5068 | (2,4086; 12,5901) |
| III | II | 1,6526 | (0,6819; 4,0049) |
| IV | II | 4,7872 | (1,7825; 12,8566) |
| IV | III | 2,8968 | (1,2952; 6,4788) |
Principais resultados: Risco Relativo, IC 95%
Passo 4: Determinar se o modelo satisfaz a suposição de riscos proporcionais
- Testes para tabela de riscos proporcionais
-
Use os testes para determinar se o modelo atende à suposição de riscos proporcionais. A hipótese nula é que o modelo atende ao pressuposto de todos os preditores. Geralmente, um nível de significância (denotado como α ou alfa) de 0,05 funciona bem. Um nível de significância de 0,05 indica um risco de 5% de concluir que o parâmetro extra melhora significativamente o ajuste de distribuição, quando, na verdade, não.
Se o valor-p for menor ou igual ao nível de significância, conclua que o modelo não especifica corretamente a relação. Se o valor p for maior ou igual ao nível de significância, não é possível concluis que o modelo explica a variação na resposta.
- Trama de Arjas
-
Use a trama de Arjas para determinar se o modelo atende à suposição de riscos proporcionais para um preditor categórico. Se as curvas na trama diferem da linha de 45 graus, então o modelo não atende à suposição de riscos proporcionais para o preditor.
Se o modelo não atender à suposição de uma variável, tente usar a variável como variável de estratificação.
- Trama de Andersen
-
Use o enredo de Andersen para determinar se o modelo atende à suposição de riscos proporcionais para diferentes estratos. Cada combinação de valores de uma ou mais variáveis de estratificação define um estrato. O enredo contém uma curva para cada estrato. Se o modelo atender à suposição, as curvas são linhas retas através do ponto onde X = 0 e Y = 0. Se a taxa de risco da linha de base para um estrato for a mesma da taxa de risco da linha de base para o estrato no eixo x, então a curva segue a linha de referência de 45 graus na trama.
Se o modelo não atender ao pressuposto, considere se deve dividir os dados pela variável estratificação para a qual o modelo não atende ao pressuposto de riscos proporcionais. Em seguida, realize uma análise separada em cada subconjunto dos dados. As análises separadas fornecem efeitos diferentes para os preditores em cada subconjunto.
Testes para riscos proporcionais
| Termo | GL | Correlação | Qui-Quadrado | Valor-P |
|---|---|---|---|---|
| Idade | 1 | 0,1328 | 1,18 | 0,278 |
| Palco | ||||
| II | 1 | -0,0104 | 0,01 | 0,940 |
| III | 1 | -0,2445 | 2,86 | 0,091 |
| IV | 1 | -0,1193 | 0,63 | 0,426 |
| Global | 4 | — | 4,61 | 0,330 |
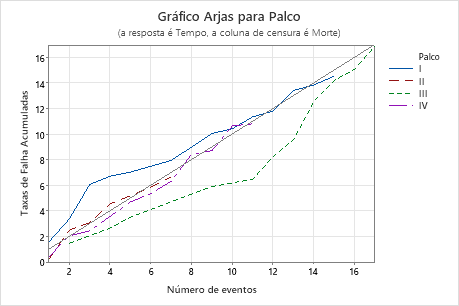
Principais resultados: Valor P, trama de Arjas
Nestes resultados, os valores p para o teste para riscos proporcionais são todos superiores a 0,05, portanto não é possível concluir que o modelo não atende ao pressuposto de riscos proporcionais.
O enredo de Arjas exibe as taxas de risco cumulativas versus o número de eventos para cada nível de Palco. Neste gráfico de Arjas, as linhas geralmente seguem a linha de 45 graus, para que você possa concluir que o modelo atende ao pressuposto de riscos proporcionais para o preditor Palco.
