Neste tópico
Os testes da suposição de riscos proporcionais no Minitab Statistical Software utilizam a abordagem de Grambsch e Therneau (1994)1.
GL
Os graus de liberdade são 1 para cada coeficiente estimado. Para o teste geral, os graus de liberdade são a soma dos graus de liberdade para os coeficientes.
Qui-quadrado
Teste global para todos os preditores
Os testes avaliam a hipótese nula de que as inclinações para todos os termos do modelo são zero para a relação entre os resíduos de Schoenfeld escalonados e uma transformação em escala temporal dos tempos de evento em relação à hipótese alternativa de que pelo menos uma inclinação não é zero.
A estatística de teste para o teste simultâneo de todos os preditores no modelo tem a seguinte forma:

Sob a hipótese nula de que a suposição de riscos proporcionais é verdadeira para todos os preditores,  é assintoticamente distribuída como uma distribuição qui-quadrado com p grau de liberdade.
é assintoticamente distribuída como uma distribuição qui-quadrado com p grau de liberdade.
Teste para preditores individuais
Os testes avaliam a hipótese nula de que a inclinação é zero para a relação entre os resíduos de Schoenfeld escalonados por um termo e uma transformação em escala temporal dos tempos de evento em relação à hipótese alternativa de que a inclinação não é zero.
A estatística de teste em relação a um preditor individual tem a seguinte forma:
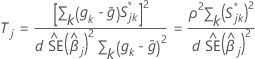
Sob a hipótese nula de que a suposição de riscos proporcionais é verdadeira para o preditor, 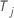 é assintoticamente distribuída como uma distribuição qui-quadrado com 1 grau de liberdade.
é assintoticamente distribuída como uma distribuição qui-quadrado com 1 grau de liberdade.
Notação
| Termo | Descrição |
|---|---|
 | os horários do evento |
| d | o número de vezes de evento |
| p | o número de termos no modelo |
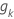 | Uma transformação em escala de tempo dos tempos de evento. A carta G no software estatístico Minitab
|
 | a matriz de variância-covariância assintótica de 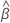 |
| S | d × p matriz dos resíduos de Schoenfeld |
| S* | d × p matriz dos resíduos de Schoenfeld escalonados |
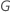 | um vetor d-dimensional cujos componentes são os valores centrados de 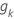 Em que Em que  |
 |  |
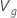 | a variância amostral dos componentes de 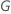 |
 | a média amostral dos componentes de 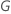 |
 | o erro padrão do componente jth do vetor 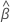 de parâmetros estimados do modelo de risco proporcional cox de parâmetros estimados do modelo de risco proporcional cox |
 | o coeficiente de correlação entre os resíduos de Schoenfeld escalonados para o preditor jth e os valores funcionais transformados no tempo, 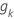 |
Valor-p
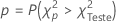
em que  é uma variável aleatória que segue uma distribuição qui-quadrado com
é uma variável aleatória que segue uma distribuição qui-quadrado com  graus de liberdade.
graus de liberdade.  A estatística de teste
A estatística de teste
