Para cada assunto 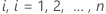 Seja
Seja  ser a função passo que representa o número de eventos que se submetem
ser a função passo que representa o número de eventos que se submetem 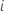 experiências até o tempo
experiências até o tempo  . Então
. Então 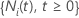 representa um processo de contagem para o assunto
representa um processo de contagem para o assunto 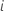 . Seja
. Seja 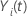 ser uma variável indicadora que tem o valor 1 se sujeito i está em risco no momento t e 0 de outra forma, o que é equivalente a
ser uma variável indicadora que tem o valor 1 se sujeito i está em risco no momento t e 0 de outra forma, o que é equivalente a 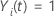 Se
Se 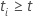 e
e 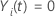 Senão
Senão
 para um indivíduo
para um indivíduo 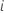 com um vetor de valores preditores
com um vetor de valores preditores 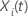 , tem a seguinte forma:
, tem a seguinte forma:
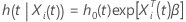
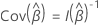
em que  é a taxa de risco da linha de base que caracteriza a distribuição não especificada do tempo de sobrevivência e
é a taxa de risco da linha de base que caracteriza a distribuição não especificada do tempo de sobrevivência e  é um vetor p-componente de coeficientes de regressão desconhecidos.
é um vetor p-componente de coeficientes de regressão desconhecidos.
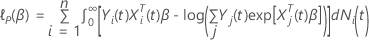
 , tem a seguinte forma:
, tem a seguinte forma:
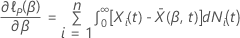
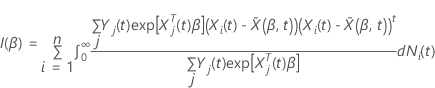
 , tem a seguinte forma:
, tem a seguinte forma:
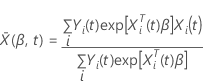
- O assunto pode vivenciar mais de um evento de interesse.
- O sujeito pode vivenciar um evento várias vezes. Essa afirmação significa que a variável indicadora que identifica se o sujeito está em risco,
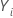 , pode mudar estados de 1 para 0 e voltar várias vezes.
, pode mudar estados de 1 para 0 e voltar várias vezes. - O sujeito pode entrar no estudo após o tempo 0. Esta afirmação equivale à ideia de que um sujeito pode entrar no conjunto de risco após o tempo 0. Um tempo é truncado quando o sujeito entra após o tempo 0.
O formulário de entrada do processo de contagem
No formulário de entrada do processo de contagem, várias linhas representam cada assunto. Cada linha descreve um intervalo de tempo quando os valores de todas as variáveis são constantes. Preditores dependentes do tempo mudam entre linhas. Os intervalos começam logo após o horário de início e incluem o tempo final. O tempo de início para o intervalo é o tempo de entrada para o assunto. O tempo final é a variável de resposta para o sujeito. A coluna de censura indica qualquer linha onde o horário final não seja um horário de evento.