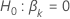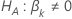Equação de Regressão
O modelo de riscos proporcionais cox semi-paramétricos usa os valores preditor para um indivíduo, 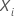 , para prever a pontuação de risco,
, para prever a pontuação de risco, 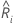 . O processo tem as seguintes etapas gerais:
. O processo tem as seguintes etapas gerais:

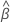 o vetor de coeficientes estimados Os coeficientes estimados podem incluir valores para termos de ordem mais elevados, como os quadrados de preditores contínuos. O escore de risco estimado é válido durante todo o período de estudo e não depende do tempo. Na saída, a equação tem a seguinte forma onde uma equação separada aparece para diferentes níveis de fatores categóricos:
o vetor de coeficientes estimados Os coeficientes estimados podem incluir valores para termos de ordem mais elevados, como os quadrados de preditores contínuos. O escore de risco estimado é válido durante todo o período de estudo e não depende do tempo. Na saída, a equação tem a seguinte forma onde uma equação separada aparece para diferentes níveis de fatores categóricos:
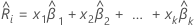
Coef.
Deixe que a função de probabilidade parcial de log para o modelo de riscos proporcionais cox seja 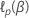 . O modelo completo maximiza a função log-verossimilhança,
. O modelo completo maximiza a função log-verossimilhança, 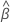 , dá os coeficientes estimados para o modelo. Achar
, dá os coeficientes estimados para o modelo. Achar 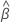 , defina os derivados parciais da função de probabilidade parcial de log igual a zero e resolva as equações para
, defina os derivados parciais da função de probabilidade parcial de log igual a zero e resolva as equações para  . Minitab Statistical Software usa o método de iteração Newton-Raphson para resolver as equações. Veja Murray (1972)1 para uma descrição do método iterativo Newton-Raphson.
. Minitab Statistical Software usa o método de iteração Newton-Raphson para resolver as equações. Veja Murray (1972)1 para uma descrição do método iterativo Newton-Raphson.
O vetor de derivativos parciais da função de probabilidade parcial de log depende se a variável de resposta inclui tempos de evento amarrados. Se a variável de resposta incluir laços, então a estimativa usa a aproximação de Efron ou a aproximação de Breslow. Se a variável resposta não tiver laços, todos os 3 métodos fornecem as mesmas estimativas. Quanto menos vínculos estão nos dados, mais próximos são os resultados dos dois métodos de aproximação. Quanto mais laços estão nos dados, mais a aproximação do Efron melhora na aproximação de Breslow.
| Termo | Descrição |
|---|---|
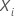 | o vetor de valores covariados que corresponde à unidade amostral com o tempo de evento 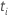 |
Dados sem vínculos
| Termo | Descrição |
|---|---|
 | o número de vezes de evento |
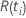 | o risco definido no momento 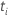 , que é o conjunto de todas as unidades amostrais que ainda não falharam antes do tempo , que é o conjunto de todas as unidades amostrais que ainda não falharam antes do tempo 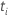 |
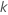 | uma variável de contagem para o número de parâmetros no modelo,  Em que Em que  o número de termos no modelo o número de termos no modelo |
A função de probabilidade parcial para o modelo de riscos proporcionais cox sem vínculos tem a seguinte forma:
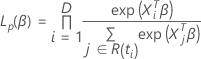
A função de perda tem a seguinte forma:
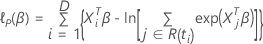
 , tem a seguinte forma:
, tem a seguinte forma:
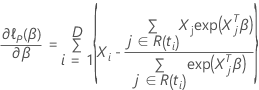
de modo que a derivada parcial para um coeficiente específico, 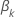 , tem a seguinte forma:
, tem a seguinte forma:
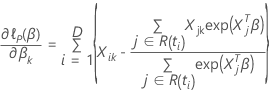
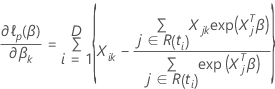
Dados com vínculos
| Termo | Descrição |
|---|---|
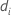 | O número de eventos entre o 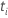 |
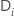 | o conjunto de todas as unidades amostrais que têm o evento no momento 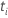 |
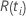 | o risco definido no momento 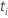 , que é o conjunto de todas as unidades amostrais que ainda não falharam antes do tempo , que é o conjunto de todas as unidades amostrais que ainda não falharam antes do tempo 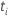 |

Aproximação da Efron para dados com vínculos
A função de perda tem a seguinte forma:
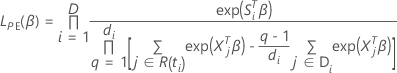
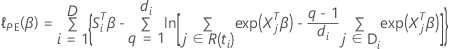
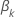 , tem a seguinte forma:
, tem a seguinte forma:
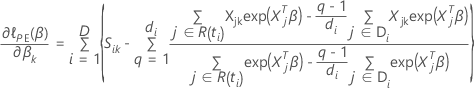
Aproximação de Breslow para dados com vínculos
A função de perda tem a seguinte forma:
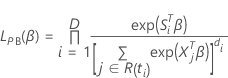
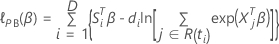
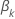 , tem a seguinte forma:
, tem a seguinte forma:
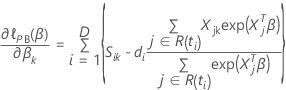
Coeficientes codificados
A tabela exibe coeficientes codificados quando a análise padroniza os preditores contínuos. Para encontrar os coeficientes codificados, substitua os preditores padronizados nas equações anteriores.
EP de Coef
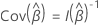
onde a matriz de informação observada,  depende de se a variável de resposta inclui tempos de evento amarrados. Se a variável de resposta incluir laços, então a estimativa usa a aproximação de Efron ou a aproximação de Breslow. Se a variável resposta não tiver laços, todos os 3 métodos fornecem as mesmas estimativas. Quanto menos vínculos estão nos dados, mais próximos são os resultados dos dois métodos de aproximação. Quanto mais laços estão nos dados, mais a aproximação do Efron melhora na aproximação de Breslow.
depende de se a variável de resposta inclui tempos de evento amarrados. Se a variável de resposta incluir laços, então a estimativa usa a aproximação de Efron ou a aproximação de Breslow. Se a variável resposta não tiver laços, todos os 3 métodos fornecem as mesmas estimativas. Quanto menos vínculos estão nos dados, mais próximos são os resultados dos dois métodos de aproximação. Quanto mais laços estão nos dados, mais a aproximação do Efron melhora na aproximação de Breslow.
Dados sem vínculos
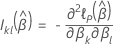
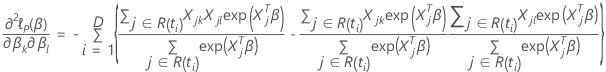
Aproximação da Efron para dados com vínculos
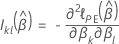
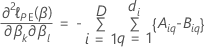
em que
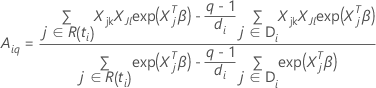
e
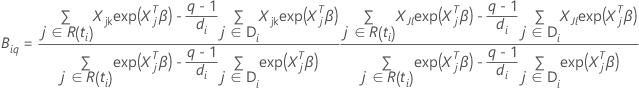
Aproximação de Breslow para dados com vínculos
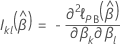
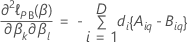
em que
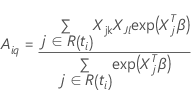
e
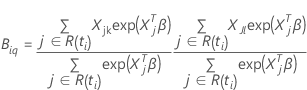
Valor Z
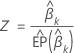
em que  O que é o erro padrão do coeficiente?
O que é o erro padrão do coeficiente? 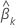 . O valor-p de
. O valor-p de  é a raiz quadrada positiva do elemento kth diagonal de
é a raiz quadrada positiva do elemento kth diagonal de  .
.
IC
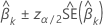
em que 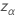 o ponto percentil superior α da distribuição normal padrão
o ponto percentil superior α da distribuição normal padrão
Valor-p

| Termo | Descrição |
|---|---|
 | uma variável aleatória da distribuição normal padrão |
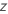 | estatística de teste para o  Definir a hipótese alternativa Definir a hipótese alternativa 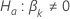 |
Modelos de riscos proporcionais estratificados
Para um modelo que inclui uma variável categórica com níveis de s como variável de estratificação, os coeficientes de regressão são constantes em todos os estratos. A estimativa dos coeficientes de regressão no modelo estratificado tem o mesmo processo do modelo de riscos proporcionais sem estratificação. Para o modelo estratificado, a função de probabilidade parcial de log tem a seguinte forma:

em que 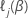 é a probabilidade parcial de registro dentro do estrato j. Soma os derivados em cada estrato para obter as equações de probabilidade parcial. Os derivados em cada estrato são os mesmos que os derivados para o modelo de riscos proporcionais sem estratificação. Os métodos Breslow e Efron aplicam-se em conformidade.
é a probabilidade parcial de registro dentro do estrato j. Soma os derivados em cada estrato para obter as equações de probabilidade parcial. Os derivados em cada estrato são os mesmos que os derivados para o modelo de riscos proporcionais sem estratificação. Os métodos Breslow e Efron aplicam-se em conformidade.