Linear

Notação
| Termo | Descrição |
|---|---|
| Yp | tempo de falha ou do log do tempo de falha |
| β0 | intercepto y (constante) |
| β1 | coeficiente de regressão |
| σ | recíproco do parâmetro de forma (distribuição Weibull) ou o parâmetro de escala (outras distribuições) |
| Φ-1(p) | the pº quantil da distribuição de vida útil padronizada |
Arrhenius

em que o valor no numerador (11604,53) é o valor invertido da constante de Boltzmann e o valor no denominador (273,16) é o 0 absoluto.
Notação
| Termo | Descrição |
|---|---|
| Yp | Tempo de falha ou do log do tempo de falha |
| β0 | intercepto y (constante) |
| β1 | coeficiente de regressão |
| σ | recíproco do parâmetro de forma (distribuição Weibull) ou o parâmetro de escala (outras distribuições) |
| Φ-1(p) | the pº quantil da distribuição de vida útil padronizada |
Temperatura inversa

Notação
| Termo | Descrição |
|---|---|
| Yp | tempo de falha ou do log do tempo de falha |
| β0 | intercepto y (constante) |
| β1 | coeficiente de regressão |
| σ | recíproco do parâmetro de forma (distribuição Weibull) ou o parâmetro de escala (outras distribuições) |
| Φ-1(p) | the pº quantil da distribuição de vida útil padronizada |
Ln (Poder)

Notação
| Termo | Descrição |
|---|---|
| Yp | tempo de falha ou do log do tempo de falha |
| β0 | intercepto y (constante) |
| β1 | coeficiente de regressão |
| σ | recíproco do parâmetro de forma (distribuição Weibull) ou o parâmetro de escala (outras distribuições) |
| Φ-1(p) | the pº quantil da distribuição de vida útil padronizada |
Modelo padronizado
A aceleração padronizada é calculada da seguinte maneira:
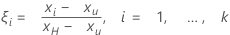
O modelo de teste de vida útil acelerado padronizado é:

Notação
| Termo | Descrição |
|---|---|
| k | número de níveis da variável de aceleração (não incluindo o nível de utilização normal) |
| Xi | nível da variável de aceleração |
| XU | nível de utilização |
| XH | nível mais alto da variável de aceleração |
