Existem duas condições que impedem a convergência das estimativas de probabilidade máxima para os coeficientes: separação completa e separação quase-completa.
Separação completa
Separação completa ocorre quando uma combinação linear dos preditores gera uma predição perfeita da variável de resposta. Por exemplo, no conjunto de dados a seguir, se X ≤ 4 então Y = 0. Se X > 4 então Y = 1.
| Y | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |
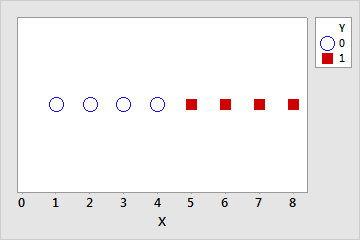
Separação quase completa
A separação quase completa é similar à separação completa. Os preditores geram uma predição perfeita da variável de resposta para a maior parte dos valores dos preditores, mas não todos. Por exemplo, no conjunto de dados anterior, onde x = 4, faça Y = 1 ao invés de 0. Agora, se X < 4 então Y = 0, se X > 4 então Y = 1, mas se X = 4 então Y poderia ser 0 ou 1. Essa sobreposição na parte central dos dados torna a separação quase completa.
| Y | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |

Causas e correção
Uma separação ocorre frequentemente quando o conjunto de dados é muito pequeno para se observar eventos com baixas probabilidades. Quanto mais preditores houver no modelo, mais provável será a separação porque os grupos individuais nos dados possuem tamanhos amostrais menores.
Embora o Minitab imprima uma advertência ao detectar separação, quanto mais preditores houver no modelo, mais difícil será identificar a causa da separação. A inclusão de termos de interação no modelo aumenta ainda mais essa dificuldade.
- Aumente a quantidade de dados. A separação ocorre frequentemente quando existe uma categoria ou intervalo de um preditor com somente um valor de resposta. Um tamanho amostral maior aumenta a probabilidade de valores diferentes para a resposta.
- Considere o significado da separação. Embora a separação completa e a separação quase completa possam indicar que o tamanho amostral é muito pequeno, elas também podem indicar relações importantes. Se a probabilidade real de um evento em um certo nível ou combinação de níveis é próxima de 0 ou 1, essa informação é importante.
- Considere um modelo alternativo. Quanto mais termos estiverem no modelo, é mais provável que a separação ocorra por pelo menos uma variável. Ao selecionar os termos do modelo, você pode verificar se a exclusão de um termo permite que as estimativas da máxima verossimilhança convirjam. Se existir um modelo útil que não usa o termo, você pode continuar a análise com o novo modelo.
- Verifique se é possível combinar categorias em variáveis problemáticas. Se existem categorias que podem ser combinadas, a separação pode desaparecer do conjunto de dados. Por exemplo, suponha que "Fruta" seja uma variável no modelo. "Uva" não possui eventos porque o número de ensaios é baixo. Combinar "Uva" e "Laranjas" na categoria "Cítricos" elimina a separação.
^^^Table : 1. Dados com separação completa Fruta Eventos Ensaios Grapefruit 0 10 Laranjas 5 100 Maçãs 25 100 Bananas 40 100 ^^^Table : 2. Dados com sobreposição Fruta Eventos Ensaios Cítricos 5 110 Maçãs 25 100 Bananas 40 100 - Verifique se uma variável categórica problemática é uma variável agregada. Se a relação da variável não agregada com a resposta não mostra separação completa, a substituição dos dados numéricos pode eliminar a separação. Por exemplo, suponha que "Tempo de serviço" seja uma variável agregada no modelo. Quando os dados estão em incrementos de 30 dias, o menor nível possui todos os eventos e o maior nível não tem eventos, criando uma separação completa. A substituição do número de dias no modelo elimina a separação.
^^^Table : 3. Dados com separação completa Categorias de tempo Eventos Ensaios 1–90 2 2 91–180 1 2 181–270 1 2 271–360 0 2 Comprimento exato Eventos Ensaios 45 1 1 60 1 1 95 1 1 176 0 1 185 0 1 241 1 1 280 0 1 299 0 1
Leitura posterior
Para obter mais informações sobre separação, consulte Albert and J. A. Anderson (1984) "On the existence of maximum likelihood estimates in logistic regression models" Biometrika 71, 1, 1–10.
