Neste tópico
Componentes da variância
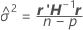
onde 

Para obter detalhes sobre a estimativa de θi, consulte [1].
Para obter mais detalhes sobre a notação, vá para a seção Métodos.
Referências
- Hemmerle, W. and Hartley, H. (1973). Computing Maximum Likelihood Estimates for the Mixed A.O.V. Model using the W transformation. Technometrics, 15(4):819–831.
Erros padrão de componentes da variância
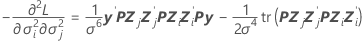
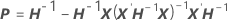
 coluna, j = 1, …, c:
coluna, j = 1, …, c:
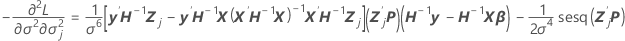

Este componente também é o valor da última coluna e a  linha pela propriedade simetria da matriz de variância-covariância.
linha pela propriedade simetria da matriz de variância-covariância.

A matriz de variância-covariância assintótica das estimativas de componentes de variância é duas vezes o inverso da matriz de informações de Fisher observada. As estimativas dos erros padrão são as raízes quadradas dos elementos diagonais da matriz de variância-covariância. Os primeiros elementos diagonais c são para os componentes de variância dos termos de efeitos aleatórios. O último elemento da diagonal é para o componente de variância de erro.
Notação
| Termo | Descrição |
|---|---|
 | o traço da matriz  |
 | a soma dos quadrados de todos os elementos na matriz M |
Para obter mais detalhes sobre a notação, vá para a seção Métodos.
Intervalos de confiança para componentes da variância
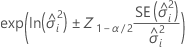
Notação
| Termo | Descrição |
|---|---|
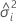 | o componente da variância para o iésimo fator aleatório |
 | o 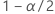 quantil da distribuição normal padrão quantil da distribuição normal padrão |
 | 1 − nível de confiança |
Valor-z e valor-p
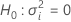
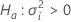


Notação
| Termo | Descrição |
|---|---|
| Z | o valor da função de distribuição acumulada para a distribuição normal padrão |
Matriz de variância-covariância
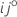 componente da matriz de informações observadas de Fisher:
componente da matriz de informações observadas de Fisher:
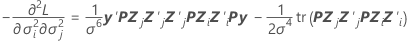

 coluna, j = 1, …, c:
coluna, j = 1, …, c:
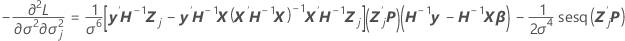

Este componente também é o valor da última coluna e a  linha pela propriedade simetria da matriz de variância-covariância.
linha pela propriedade simetria da matriz de variância-covariância.

Notação
| Termo | Descrição |
|---|---|
 | o traço da matriz  |
Para obter mais detalhes sobre a notação, vá para a seção Métodos.
