Métodos e fórmulas para Estudo de estabilidade para lotes aleatórios

Selecione o método de sua escolha.

Neste tópico

O modelo misto e a log-verossimilhança
Transformação Box-Cox
Seleção de modelo de lote aleatório

O modelo misto e a log-verossimilhança

A forma geral do modelo misto

Os modelos de efeito misto contêm efeitos fixos e aleatórios. A forma geral do modelo de efeito misto é:

y = Xβ + Z₁μ₁+ Z₂μ₂ + ... + Z_cμ_c + ε

Notação

Termo	Descrição
y	o vetor n x 1 dos valores de resposta
X	a matriz de planejamento n x p dos efeitos fixos, p ≤ n
Z_i	a matriz de planejamento n x m_i do i^ésimo efeito aleatório no modelo
β	um vetor p x 1 de parâmetros desconhecidos
μ_i	um vetor m_i x 1 de variáveis independentes de N(0, σ²_i)
ε	um n x 1 vetor de variáveis independentes de N(0, σ²_i)
c	o número de efeitos aleatórios no modelo

Formas particulares do modelo misto

Os estudos de estabilidade ajustam dois modelos com um fator de lote aleatório. O modelo maior contém a hora, o fator de lote aleatório e a interação aleatória entre a hora e o lote.

y = Xβ + Z₁μ₁+ Z₂μ₂ + ε

O modelo menor contém a hora e o fator de lote aleatório.

y = Xβ + Z₁μ₁+ε

A matriz de variância-covariância geral do vetor de resposta, y, é:

V(σ²) = V(σ², σ²₁, ... , σ²_c) = σ²I_n + σ²₁Z₁Z'₁ + ... + σ²_cZ_cZ'_c

onde

σ² = (σ², σ²₁, ... , σ²_c)'

σ², σ²₁, ... , σ²_c são chamados componentes de variância.

Por fatoração da variância, você pode encontrar uma representação de H(θ), que está no cálculo da log-verossimilhança dos modelos mistos.

V(σ²) = σ²H(θ) = σ²[I_n + θ₁Z₁Z'₁ + ... + θ_cZ_cZ'_c]

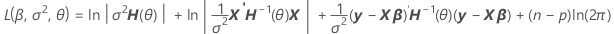
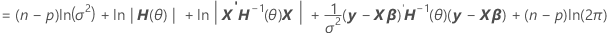
Quando o lote é um fator aleatório, as estimativas de parâmetro desconhecido vêm da minimização em dobro do negativo da função de log-verossimilhança restrita. A minimização é equivalente à maximização da função de log-verossimilhança restrita. A função para minimizar é:

Notação

Termo	Descrição
n	o número de observações
p	o número de parâmetros em β, 2 para estudos de estabilidade
σ²	o erro do componente de variância
X	a matriz do experimento –– para termos fixos, a constante e o tempo
H(θ)	I_n + θ₁Z₁Z'₁ + ... + θ_cZ_cZ'_c
I_n	a matriz de identidade com n linhas e colunas
θ_i	a razão da variância para o i^ésimo termo aleatório sobre a variância do erro
Z_i	a matriz n x m_i de codificações conhecidas para o i^ésimo efeito aleatório no modelo
m_i	o número de níveis para o i^ésimo efeito aleatório
c	o número de efeitos aleatórios no modelo
\|H(θ)\|	o determinante de H(θ)
X'	a transposição do X
H^-1(θ)	o inverso de H(θ)

Transformação Box-Cox

A transformação de Box-Cox seleciona valores de lambda, conforme mostrado a seguir, que minimizam a soma dos quadrados dos resíduos. A transformação resultante é Y ^λ quando λ ≠ 0 e ln(Y) quando λ = 0. Quando λ < 0, o Minitab também multiplica a resposta transformada por -1 para manter a ordem da resposta não transformada.

O Minitab pesquisa um valor ideal entre −2 e 2. Os valores que estão fora desse intervalo podem não resultar em um ajuste melhor.

A seguir estão algumas transformações comuns onde Y é a transformação dos dados Y:

Valor lambda (λ)	Transformação
λ = 2	Y′ = Y ²
λ = 0,5	Y′ =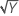
λ = 0	Y′ = ln(Y )
λ = −0,5
λ = −1	Y′ = −1 / Y

Seleção de modelo de lote aleatório

A seleção do modelo determina se a validade depende do lote e se o efeito do tempo depende do lote. O Minitab considera os seguintes três modelos em sequência:

Tempo + Lote + Lote*Tempo (inclinações e interceptos desiguais para lotes)
Tempo + Lote (inclinações iguais e interceptos desiguais para lotes)
Tempo (inclinações e interceptos iguais para lotes)

Se a interação Lote*Tempo for significativa, a análise ajusta o primeiro modelo. Se a interação não for significativa, mas o termo do Lote for significativo no segundo modelo, a análise ajusta o segundo modelo. Caso contrário, a análise ajusta o terceiro modelo.

O teste para se deseja criar pool de lotes é ligeiramente diferente do teste para incluir lote, apesar de ambos dependerem da distribuição qui-quadrado. As fórmulas das estatísticas de teste e valores-p são as seguintes.

Teste entre modelo 1 e modelo 2

diferença - −2L₂ − (−2L₁)

p = 0,5 * Prob(χ²₁ > diferença) + 0,5 * Prob(χ²₂ > diferença)

Teste entre o modelo 2 e o modelo 3

diferença = −2L₃ − (−2L₂)

p = 0,5 * Prob(χ²₁ > diferença)

Notação

Termo	Descrição
L_a	a log-verossimilhança do modelo a
p	o valor-p para o teste
Prob(χ²₁> diferença)	A probabilidade de que uma variável aleatória de uma distribuição qui-quadrado com 1 grau de liberdade seja maior do que a diferença
Prob(χ²₂> diferença)	a probabilidade de que uma variável aleatória de uma distribuição qui-quadrado com 2 graus de liberdade seja maior do que a diferença

Referências

Searle, S.R. Casella, G. and McCuloch, C.E. (1992). Variance Components
West, B.T., Welch, K.B. and Galecki, A.T. (2007). Linear Mixed Models: A Practical Guide Using Statistical Software.
Chow, S. (2007). Statistical Design and Analysis of Stability Studies.