Neste tópico
Valor ajustado
O Y predito ou 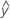 ; o valor da resposta média para os dados valores da preditora usando-se a equação de regressão estimada.
; o valor da resposta média para os dados valores da preditora usando-se a equação de regressão estimada.
Erro padrão de valor ajustado marginal (SE Fit)
O erro padrão dos valores ajustados marginais no modelo misto depende do método de teste para os efeitos fixos. Para ambos os métodos, os erros padrão são as raízes quadradas dos elementos da diagonal da matriz de variância dos ajustes.
Método de Kenward-Roger

onde
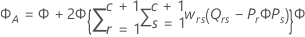
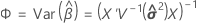
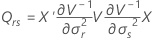
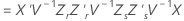
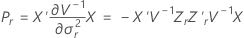
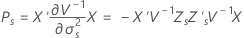
Aproximação de Satterthwaites

onde
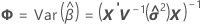
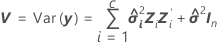
Resíduos
Um resíduo é a diferença entre um valor observado e um valor ajustado. Esta parte da observação não está explicada pelo modelo ajustado. O resíduo de uma observação é:
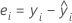
Quando o lote é um fator aleatório, o Minitab calcula 2 tipos de resíduos. Resíduos marginais usam o valor ajustado para um lote aleatório, de forma que o coeficiente do lote não está na equação.
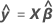
Os resíduos condicionais usam o valor ajustado para um lote que está nos dados.
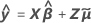
Notação
| Termo | Descrição |
|---|---|
| yi | iésimo valor de resposta observado |
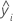 | iésimo valor de resposta ajustado |
 | o vetor das respostas ajustadas |
| X | a matriz de planejamento dos efeitos fixos |
 | o vetor das preditoras fixas |
| Z | a matriz de planejamentos dos fatores aleatórios |
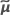 | o vetor dos valores BLUP estimados |
Resíduos padronizados

onde o desvio padrão do resíduo é a raiz quadrada diagonal apropriada da matriz de variância residual:
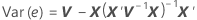
onde
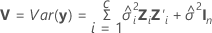
Notação
| Termo | Descrição |
|---|---|
| ei | o iésimo resíduo |
| Std(ei) | o desvio padrão do iésimo resíduo |
Intervalo de confiança
A amplitude na qual espera-se que a resposta média estimada de um dado conjunto de valores da preditora caia.


onde
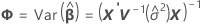
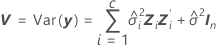
Os graus de liberdade usam esta fórmula quando o lote é um fator aleatório.
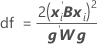
onde

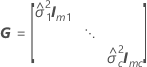
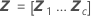
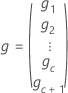

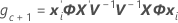
Notação
| Termo | Descrição |
|---|---|
| t1-α/2, df | 1–α/2 quantil da distribuição t com os dados graus de liberdade |
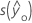 | erro padrão do valor ajustado |
| X | matriz de planejamento, incluindo a constante |
| X' | transposição de X |
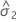 | o componente da variância para erro |
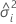 | o componente da variância do iésimo fator aleatório |
| Zi | n x mi matriz de codificações conhecidas para o iésimo efeito aleatório no modelo |
| Zi' | transposição de Zi |
| In | a matriz de identidade com n linhas e colunas |
| xi | os valores da preditora para o ajuste ou a predição |
| W | a matriz de variância-covariância assintótica do componente da variância para erro |
| c | o número de efeitos aleatórios no modelo |
Intervalo de predição
O intervalo no qual a resposta predita para uma única nova observação é esperado que caia. O cálculo do intervalo de predição depende se você calcula o intervalo para o ajuste marginal ou para o ajuste condicional.
Ajuste marginal

onde
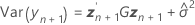

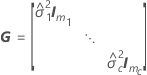
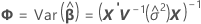
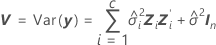
Os graus de liberdade da estatística-t são dados por esta fórmula:
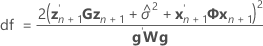
onde
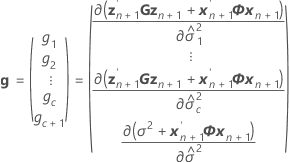


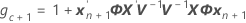
Ajuste condicional

onde
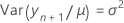
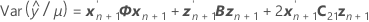
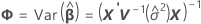
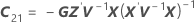
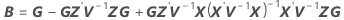
Os graus de liberdade da estatística-t são:
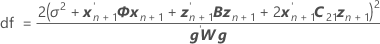
onde
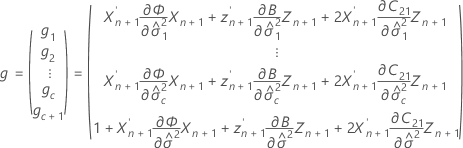

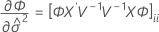
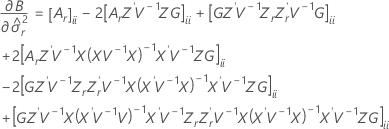
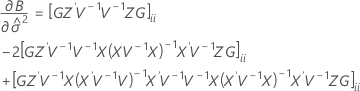
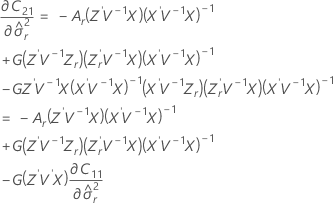
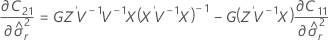
Notação
| Termo | Descrição |
|---|---|
 | 1–α/2 quantil da distribuição t com os dados graus de liberdade |
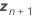 | vetor dos novos valores das preditoras aleatórias |
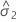 | o componente da variância para erro |
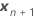 | vetor dos novos valores das preditoras fixas |
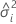 | o componente da variância do iésimo fator aleatório |
| Im | a matriz de identidade com m linhas e colunas |
| m | número de colunas na matriz de planejamento para representar o iésimo termo aleatório no modelo |
| c | o número de efeitos aleatórios no modelo |
| Zi | a matriz de planejamento n x mi do iésimo efeito aleatório no modelo |
| Z'i | transposição de Z |
