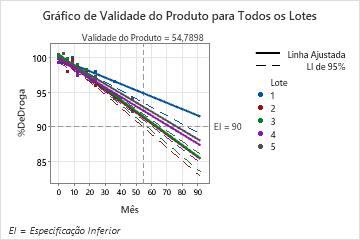
Exemplo de Estudo de estabilidade com um fator de lote fixo

Um engenheiro de qualidade de uma empresa farmacêutica deseja determinar o prazo de validade de pílulas que contêm um novo medicamento. A concentração da droga nos comprimidos diminui com o tempo. O engenheiro quer determinar quando os comprimidos atingem 90% da concentração pretendida. Por se tratar de um medicamento novo, a empresa tem apenas 5 lotes piloto para usar para estimar a vida útil. O engenheiro testa um comprimido de cada lote em nove momentos diferentes.

Para estimar a vida útil, o engenheiro faz um estudo de estabilidade. Como o engenheiro extrai amostra de todas os lotes, lote é um fator fixo em vez de um fator aleatório.

Abra os dados amostrais, PrazoDeValidade.MWX.
Escolha Estat > Regressão > Estudo de estabilidade > Estudo de estabilidade.
Selecione O lote é um fator fixo.
Em Resposta, digite %DeDroga.
Em Tempo, digite Mês.
Em Lote, digite Lote.
Em Espec inferior, insira 90.
Clique em Gráficos.
Em Gráfico de validade do produto, na segunda lista suspensa, selecione Nenhum gráfico para lotes individuais.
Em Gráficos de Resíduos, selecione Quatro em um.
Clique em OK em cada caixa de diálogo.

Interpretar os resultados

Para seguir as diretrizes de 2003 da International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use (ICH), o engenheiro seleciona um valor-p de 0,25 para termos a incluir no modelo. O valor-p da interação Mês por lote é 0,048. Como o valor-p é menor que o nível de significância de 0,25, o engenheiro conclui que as inclinações nas equações de regressão de cada lote são diferentes. O lote 3 tem a inclinação mais acentuada, -0,1630, indicando que a concentração diminui mais rápido no Lote 3. O lote 2 tem o prazo de validade mais curto, 54,79, portanto, o prazo de validade geral é o prazo de validade do lote 2.

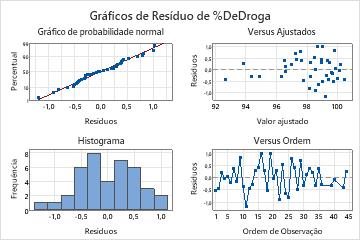
Os resíduos estão adequadamente normais e aleatoriamente dispersos em torno de 0. No gráfico de resíduos versus ajustes, menos pontos estão no lado esquerdo do gráfico do que no lado direito. Este padrão ocorre porque o engenheiro de qualidade coletou mais dados anteriormente no estudo quando as concentrações estavam altas. Este padrão não é uma violação das suposições da análise.

Fonte	GL	SQ Seq	QM Seq.	Valor F	Valor-P
Mês	1	122,460	122,460	345,93	0,000
Lote	4	2,587	0,647	1,83	0,150
Mês*Lote	4	3,850	0,962	2,72	0,048
Erro	30	10,620	0,354
Total	39	139,516

Termo	Coef	EP de Coef	Valor-T	Valor-P	VIF
Constante	100,085	0,143	701,82	0,000
Mês	-0,13633	0,00769	-17,74	0,000	1,07
Lote
1	-0,232	0,292	-0,80	0,432	3,85
2	0,068	0,292	0,23	0,818	3,85
3	0,394	0,275	1,43	0,162	3,41
4	-0,317	0,292	-1,08	0,287	3,85
5	0,088	0,275	0,32	0,752	*
Mês*Lote
1	0,0454	0,0164	2,76	0,010	4,52
2	-0,0241	0,0164	-1,47	0,152	4,52
3	-0,0267	0,0136	-1,96	0,060	3,65
4	0,0014	0,0164	0,08	0,935	4,52
5	0,0040	0,0136	0,30	0,769	*

Obs.	%DeDroga	Ajuste	Resíd	Resíd Pad
11	98,001	99,190	-1,189	-2,21	R
43	92,242	92,655	-0,413	-1,47		X
44	94,069	93,823	0,246	0,87		X

Lote	Validade do Produto
1	83,552
2	54,790
3	57,492
4	60,898
5	66,854
Global	54,790

Exemplo de Estudo de estabilidade com um fator de lote fixo

Interpretar os resultados

Método

Informações dos Fatores

Seleção de Modelo com α = 0,25

Sumário do Modelo

Coeficientes

Equação de Regressão

Ajustados e Diagnósticos para Observações Atípicas

Estimação da Validade do Produto

Lote
1	%DeDroga	=	99,853 - 0,0909 Mês

2	%DeDroga	=	100,153 - 0,1605 Mês

3	%DeDroga	=	100,479 - 0,1630 Mês

4	%DeDroga	=	99,769 - 0,1350 Mês

5	%DeDroga	=	100,173 - 0,1323 Mês