Neste tópico
Equação de regressão
Use a equação de regressão, para descrever a relação entre a resposta e os termos no modelo. A equação de regressão é uma representação algébrica da linha de regressão. A equação de regressão para o modelo linear assume a seguinte forma: Y= b0 + b1x1. Na equação de regressão, Y é a variável de resposta, b0 é a constante ou intercepto, b1 é o valor do coeficiente do termo linear (também conhecido como inclinação da linha), e x1 é o valor do termo.
A equação de regressão com mais de um termo toma a seguinte forma:
y = b0 + b1X1 + b2X2 + ... + bkXk
- y é a variável de resposta
- b0 é a constante
- b1, b2, ..., bk são os coeficientes
- X1, X2, ..., Xk são os valores do termo
Se o modelo contiver ambas as variáveis contínuas e categóricas, a tabela de equação de regressão pode exibir uma equação para cada combinação de níveis para as variáveis categóricas. Para utilizar essas equações para predição, você deve escolher a equação correta com base nos valores das variáveis categóricas e, em seguida, digitar os valores das variáveis contínuas.
Configurações variáveis
O modelo usa as configurações para as variáveis para calcular as predições. Se as configurações de variáveis são incomuns comparadas aos dados que o Minitab usou para estimar o modelo, o Minitab exibe um aviso abaixo da predição.
Ajuste
Os valores ajustados também são chamados de ajustes ou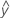 
. Os valores ajustados são estimativas de ponto da resposta média para dados valores das preditoras. Os valores das preditoras também são chamados de valores-x.
Interpretação
Valores ajustados são calculados inserindo os valores x específicos para cada observação no conjunto de dados para o modelo da equação.
Por exemplo, se a equação for y = 5 + 10x, o valor ajustado do valor-x, 2, é 25 (25 = 5 + 10(2)).
O Minitab registra as predições com valores incomuns da preditora comparados ao valores nos dados. Somente testes adicionais com amostras mais antigas podem confirmar que a estimativa da vida útil é exata.
Ajuste SE
O erro padrão do ajuste (EP fit) estima a variação na resposta da média estimada para as configurações de variável especificadas. O cálculo do intervalo de confiança para a resposta média usa o erro padrão do ajuste. Os erros padrão são sempre não negativos.
Interpretação
Use o erro padrão do ajuste para medir a exatidão da estimativa da resposta média. Quanto menor o erro padrão, mais precisa é a resposta média predita. Por exemplo, um analista desenvolve um modelo para predizer o tempo de entrega. Para um conjunto de configurações de variável, o modelo prediz um tempo de entrega médio de 3,80 dias. O erro padrão do ajuste para estas configurações é 0,08 dias. Para o segundo conjunto de configurações de variáveis, o modelo produz o mesmo tempo de entrega médio, com um erro padrão de ajuste de 0,02 dias. O analista pode ter mais confiança de que o tempo médio de entrega para o segundo conjunto de configurações de variáveis está próximo de 3,80 dias.
Com o valor ajustado, é possível usar o erro padrão do ajuste para criar um intervalo de confiança para a resposta média. Por exemplo, dependendo do número de graus de liberdade, um intervalo de confiança de 95% se estende cerca de dois desvios padrão acima e abaixo da média prevista. Para os tempos de entrega, o intervalo de confiança de 95% para a média prevista de 3,80 dias, quando o erro padrão é de 0,08 é (3,64, 3,96) dias. Você pode ter 95% de confiança de que a média da população está dentro deste intervalo. Quando o erro padrão é de 0,02, o intervalo de confiança de 95% é (3,76, 3,84) dias. O intervalo de confiança para o segundo conjunto de definições de variáveis é mais estreito, porque o erro padrão é menor.
Intervalo de confiança para ajuste (IC de 95%)
Esses intervalos de confiança (IC) são faixas de valores que tendem a conter a resposta média para a população que tem os valores observados dos preditores ou fatores no modelo.
Como as amostras são aleatórias, é improvável que duas amostras de uma população produzam intervalos de confiança idênticos. Mas, se você extrair amostras várias vezes, uma determinada porcentagem dos intervalos de confiança resultantes conterá o parâmetro populacional desconhecido. A porcentagem destes intervalos de confiança que contém o parâmetro é o nível de confiança do intervalo.
O intervalo de confiança é composto pelas duas partes a seguir:
Interpretação
Use o intervalo de confiança para avaliar a estimativa do valor ajustado para os valores observados das variáveis.
Por exemplo, com um nível de confiança de 95%, é possível ter 95% de certeza de que o intervalo de confiança contém a média da população para os valores especificados para as variáveis preditoras ou fatores no modelo. O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação. Um intervalo de confiança amplo indica que você pode ter menos confiança sobre a média de valores futuros. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra.
PI de 95%
O intervalo de predição é um intervalo que provavelmente contém uma única resposta futura para uma combinação selecionada de configurações de variável. O intervalo de predição é sempre mais amplo que o intervalo de confiança correspondente.
Interpretação
Por exemplo, um engenheiro de qualidade determinou que a validade de um novo medicamento é 54,79 meses. A validade desta análise é definida como a hora em que o engenheiro não pode mais ter 95% de confiança de que a concentração do pior lote é 90% da concentração pretendida. O engenheiro quer prever a concentração média do pior lote em 54,79 meses.
Nesses resultados, a predição da resposta média é de cerca de 91,36%. Contudo, o engenheiro também quer estimar a amplitude de valores para uma única cápsula do Lote 2. O intervalo de predição indica que você pode ter 95% de confiança de que a concentração predita para uma única cápsula do Lote 2 em 54,79 meses está entre aproximadamente 89,3217% e 93.4001%.
Configurações
| Variável | Configuração |
|---|---|
| Mês | 54,79 |
| Lote | 2 |
Predição
| Ajuste | EP do Ajustado | IC de 95% | IP de 95% | |
|---|---|---|---|---|
| 91,3609 | 0,801867 | (89,7233; 92,9986) | (89,3217; 93,4001) | XX |
