Neste tópico
Coeficientes e coeficientes padronizados
Os coeficientes são os parâmetros em uma equação de regressão. Os coeficientes são usados com as preditoras para calcular o valor ajustado da variável de resposta e a resposta predita das novas observações. Em contraste com os mínimos quadrados, os coeficientes de PLS são estimadores não-lineares. Os coeficientes padronizados indicam a importância de cada preditora no modelo e na correspondência para as variáveis x e y padronizadas. Nos PLS, a matriz do coeficiente (dimensão p × r) é calculada a partir dos pesos e cargas fatoriais.
A fórmula dos coeficientes padronizados é:

Para calcular os coeficientes não-padronizados e o intercepto, use essas fórmulas:
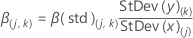

Notação
| Termo | Descrição |
|---|---|
| W | a matriz-x de peso |
| P | a matriz de cargas fatoriais-x |
| C | a matriz de cargas fatoriais-y |
| j | as preditoras (1, p) |
| k | as respostas (1, r) |
| p | o número de preditoras |
| r | o número de respostas |
Leverages
Na regressão de mínimos quadrados, os leverages são valores que indicam quão longe as observações correspondentes estão do centro do espaço-x, que está descrito pelos valores-x. No PLS, as preditoras são substituídas pelos escores-x. As observações com alto leverage têm escores-x distantes de zero e têm uma influência significativa nos coeficientes de regressão. Os pontos com alto leverage são outliers no espaço-x, mas não são necessariamente outliers no espaço-y.
Os valores de leverage no PLS são calculados da matriz T do escore-x, que é usado para calcular a matriz de chapéu (H) da seguinte maneira:

O leverage (hii) da iésima observação é o iésimo elemento diagonal da matriz H.
Um valor de leverage maior do que 2 m / n é considerado alto e deve ser examinado.
Notação
| Termo | Descrição |
|---|---|
| n | o número de observações |
| m | o número de componentes |
Distâncias do modelo-x
Uma medição de quão bem as observações são ajustadas no espaço-x, indica quão bem as observações descrevem escores-x. Uma observação com uma grande distância também pode ser um ponto de leverage.
Fórmula
A fórmula para calcular a distância do modelo-x para a iésima observação é a seguinte:
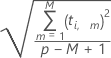
Notação
| Termo | Descrição |
|---|---|
| M | número de componentes |
| t | escore-x |
| p | número de preditoras |
Distâncias do modelo y
Uma medição de quão bem as observações são ajustadas no espaço-y, indica quão bem as observações descrevem escores-y. Uma observação com uma grande distância também pode ser um outlier.
Fórmula
A fórmula para calcular a distância do modelo-y para a iésima observação é a seguinte:
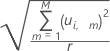
Notação
| Termo | Descrição |
|---|---|
| M | o número de componentes |
| u | o escore-y |
| r | o número de respostas |
