Neste tópico
Escores-x
Os escores-x são combinações lineares dos termos; similares aos escores dos componentes principais. Os escores-x formam uma matriz n × m de colunas não-correlacionadas. Os escores-x são projeções das observações sobre os componentes do PLS. O PLS se ajusta aos escores-x, que substituem os termos originais nos dados, usando a estimativa de mínimos quadrados.
Fórmula
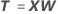
Notação
| Termo | Descrição |
|---|---|
| n | o número de observações |
| m | o número de componentes |
| i | as observações de 1 a n |
| j | os termos de 1 a p |
| X | a matriz de experimento |
| W | a matriz-x de peso |
Cargas fatoriais-x
As cargas fatoriais-x são coeficientes lineares que ligam os termos aos escores-x, similares aos autovetores na análise dos principais componentes. O valores de cargas fatoriais indicam a importância do termo correspondente ao mésimo componente. As cargas fatoriais-x formam uma matriz p × m.
Fórmula
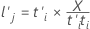
Notação
| Termo | Descrição |
|---|---|
| p | o número de termos |
| m | o número de componentes |
| i | as observações de 1 a n |
| j | os termos de 1 a p |
| t | os escores-x |
| X | as preditoras |
Pesos-x
Os pesos-x descrevem a covariância entre os termos e as respostas. No algoritmo, os pesos asseguram que os escores-x sejam ortogonais ou não-relacionados uns aos outros, e são usados para calcular os escores-x. Os pesos-x formam uma matriz p × m.
Fórmula
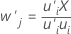
O Minitab escala o vetor de pesos de forma que o comprimento do vetor seja 1.
Notação
| Termo | Descrição |
|---|---|
| p | o número de termos |
| m | o número de componentes |
| i | as observações de 1 a n |
| j | os termos de 1 a p |
| X | a matriz de resíduos-x |
| u | os escores-y |
Resíduos-x
Os resíduos-x contêm a variância nas preditoras não explicada pelo modelo PLS. As observações com resíduos-x relativamente grandes são outliers no espaço-x, indicando que eles não são bem explicados pelo modelo.
Os resíduos-x são as diferenças entre os valores reais das preditoras e os valores-x calculados, e estão na mesma escala das preditoras originais. A matriz dos resíduos-x, similar à matriz-x original, é uma matriz n × p.
A matriz de resíduos-x é inicializada para a matriz-x padronizada. Depois de calcular o mésimo componente e obter o vetor escore-x e o vetor de cargas fatoriais-x, o Minitab calcula os resíduos-x calculados.
Fórmula

O Minitab calcula os resíduos-x não-padronizados multiplicando os resíduos-x padronizados pelo desvio padrão dos valores da preditora.
Notação
| Termo | Descrição |
|---|---|
| n | o número de observações |
| p | o número de termos |
| i | as observações de 1 a n |
| j | os termos de 1 a p |
| t | os escores-x |
| l | as cargas fatoriais-x |
Valores-x calculados
Os valores-x calculados são combinações lineares dos escores-x; contêm a variância nas preditoras explicadas pelo modelo PLS. As observações com valores-x relativamente pequenos calculados são outliers no espaço-x e não são bem explicados pelo modelo.
A matriz-x calculada, similar à matriz-x original, é uma matriz n × p, onde n é igual ao número de observações e p é igual ao número de preditoras. Os valores-x calculados estão na mesma escala que as preditoras.
A matriz-x calculada é inicializada para matriz zero. Depois de calcular o mésimo componente e obter o vetor escore-x e o vetor de cargas fatoriais-x, o Minitab calcula os valores-x calculados. Se o número de componentes for igual ao número de preditoras, o valor-x calculado será igual ao valor-x original.
Fórmula
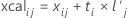
O Minitab calcula os valores-x calculados não-padronizados multiplicando os valores-x calculados padronizados pelo desvio padrão dos valores da preditora e adicionando a média.
Notação
| Termo | Descrição |
|---|---|
| n | o número de observações |
| p | o número de preditoras |
| i | o número de observações de 1 a n |
| j | o número de preditoras de 1 a p |
| t | os escores-x |
| l | as cargas fatoriais-x |
Escores-y
Os escores-y são combinações lineares das variáveis de resposta. As pontuações y formam uma matriz n x m. Os escores y são projeções das observações sobre os componentes do PLS.
Fórmula
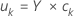
Notação
| Termo | Descrição |
|---|---|
| n | o número de observações |
| m | o número de componentes |
| k | o número de respostas de 1 a r |
| Y | a matriz-y |
| c | as cargas fatoriais-y |
Cargas fatoriais-y
As cargas fatoriais-y são coeficientes lineares que ligam as respostas aos escores-y. O valores de cargas fatoriais indicam a importância da resposta correspondente ao mésimo componente. As cargas fatoriais-y formam uma matriz r × m.
Fórmula

Notação
| Termo | Descrição |
|---|---|
| r | o número de respostas |
| m | o número de componentes |
| i | as observações de 1 a n |
| k | as respostas de 1 a r |
| Y | as respostas |
| t | os escores-x |
Resíduos-y
Os resíduos-y contêm a variância restante nas respostas não explicadas pelo modelo PLS. As observações com resíduos-y relativamente grandes são outliers no espaço-y, indicando que eles não são bem explicados.
Os resíduos-y são as diferenças entre os valores reais das respostas e os valores-y calculados, e estão na mesma escala das respostas originais. A matriz dos resíduos-y, similar à matriz-y original, é uma matriz n × r .
A matriz de resíduos-y é inicialmente definida para a matriz Y padronizada. Depois que o Minitab calcula o mésimo componente e obtém os vetores escore-x e cargas fatoriais-y, o Minitab determina os resíduos-y padronizados.
Fórmula

O Minitab estão calcula os resíduos-y padronizados multiplicando os resíduos-y padronizados pelo desvio padrão dos valores de resposta correspondentes.
Notação
| Termo | Descrição |
|---|---|
| n | o número de observações |
| r | o número de respostas |
| i | as observações de 1 a n |
| k | as respostas de 1 a r |
| t | os escores-x |
| c | as cargas fatoriais-y |
Valores calculados de Y
Os valores-y calculados são combinações lineares dos escores-x; contêm a variância nas respostas explicadas pelo modelo PLS. As observações com valores-y relativamente pequenos calculados são outliers no espaço-y e não são bem explicados.
A matriz-y calculada, similar à matriz-y original, é uma matriz n x r . A matriz-y calculada é inicialmente definida para matriz zero. Depois que o Minitab calcula o mésimo componente e obtém os vetores escore-x e cargas fatoriais-y, o Minitab determina os valores-y calculados padronizados.
Fórmula
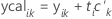
O Minitab calcula os valores-y calculados não-padronizados multiplicando os valores-y calculados padronizados pelo desvio padrão da resposta correspondente e adicionando a média.
Notação
| Termo | Descrição |
|---|---|
| n | o número de observações |
| r | o número de respostas |
| i | as observações de 1 a n |
| k | as respostas de 1 a r |
| t | os escores-x |
| c | as cargas fatoriais-y |
