Neste tópico
Ajustes
Os valores ajustados também são chamados de ajustes ou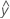 
. Os valores ajustados são estimativas de ponto da resposta média para dados valores das preditoras. Os valores das preditoras também são chamados de valores-x.
Interpretação
Valores ajustados são calculados inserindo os valores x específicos para cada observação no conjunto de dados para o modelo da equação.
Por exemplo, se a equação for y = 5 + 10x, o valor ajustado do valor-x, 2, é 25 (25 = 5 + 10(2)).
Ajuste SE
O erro padrão do ajuste (EP fit) estima a variação na resposta da média estimada para as configurações de variável especificadas. O cálculo do intervalo de confiança para a resposta média usa o erro padrão do ajuste. Os erros padrão são sempre não negativos.
Interpretação
Use o erro padrão do ajuste para medir a exatidão da estimativa da resposta média. Quanto menor o erro padrão, mais precisa é a resposta média predita. Por exemplo, um analista desenvolve um modelo para predizer o tempo de entrega. Para um conjunto de configurações de variável, o modelo prediz um tempo de entrega médio de 3,80 dias. O erro padrão do ajuste para estas configurações é 0,08 dias. Para o segundo conjunto de configurações de variáveis, o modelo produz o mesmo tempo de entrega médio, com um erro padrão de ajuste de 0,02 dias. O analista pode ter mais confiança de que o tempo médio de entrega para o segundo conjunto de configurações de variáveis está próximo de 3,80 dias.
Com o valor ajustado, é possível usar o erro padrão do ajuste para criar um intervalo de confiança para a resposta média. Por exemplo, dependendo do número de graus de liberdade, um intervalo de confiança de 95% se estende cerca de dois desvios padrão acima e abaixo da média prevista. Para os tempos de entrega, o intervalo de confiança de 95% para a média prevista de 3,80 dias, quando o erro padrão é de 0,08 é (3,64, 3,96) dias. Você pode ter 95% de confiança de que a média da população está dentro deste intervalo. Quando o erro padrão é de 0,02, o intervalo de confiança de 95% é (3,76, 3,84) dias. O intervalo de confiança para o segundo conjunto de definições de variáveis é mais estreito, porque o erro padrão é menor.
IC de 95%
O intervalo de confiança do ajuste fornece um intervalo de valores prováveis para a resposta média dadas as configurações especificadas das preditoras.
Interpretação
Use o intervalo de confiança para avaliar a estimativa do valor ajustado para os valores observados das variáveis.
Por exemplo, com um nível de confiança de 95%, você pode ter 95% de confiança de que o intervalo de confiança contém a média da população para os valores especificados das variáveis no modelo. O intervalo de confiança ajuda a avaliar a significância prática de seus resultados. Use seu conhecimento especializado para determinar se o intervalo de confiança inclui valores que tenham significância prática para a sua situação. Um amplo intervalo de confiança indica que você pode estar menos confiante sobre a média de valores futuros. Se o intervalo for muito amplo para ser útil, pense em aumentar o tamanho da amostra.
PI de 95%
O intervalo de predição é um intervalo que provavelmente contém uma única resposta futura para um valor de variável da preditora.
Interpretação
Com o intervalo de predição de 95%, você pode ter 95% de confiança de que novas observações cairão no intervalo. (Observe, contudo, que isso só é verdade para valores que estão incluídos dentro do intervalo dos dados na análise). O intervalo é definido por limites superior e inferior, que são calculados a partir do nível de confiança e do erro padrão da predição. O intervalo de predição é sempre mais amplo que o intervalo de confiança devido à incerteza adicionada envolvida na predição de uma única resposta versus a resposta média.
R2 do teste
O R2 do teste representa a proporção de variação nas respostas explicadas pelo modelo original usando valores da preditora dos dados de teste.
O conjunto de dados de teste deve incluir o mesmo número de preditoras que o conjunto de dados original. O R2 do teste só pode ser calculado quando os dados de teste incluem dados de resposta para cada observação. O R2 do teste é calculado da mesma forma que R2.
Interpretação
O teste R2 avalia como o modelo de regressão PLS prediz os dados de teste. Valores elevados de R2 de teste indicam que o modelo tem maior capacidade preditiva.
Frequentemente, a regressão PLS é executada em duas etapas. A primeira etapa, algumas vezes chamada treinamento, envolve o cálculo de um modelo de regressão PLS para um conjunto de dados de amostra (conjunto de dados de treinamento). A segunda etapa consiste em validar esse modelo com um conjunto de dados diferente, frequentemente chamado conjunto de dados de teste. Alguns conjuntos de dados de teste incluem valores de resposta, outros não. Se o conjunto de dados de teste inclui valores de resposta, o Minitab pode calcular um teste R2.
Se você usar a validação cruzada, comparar o teste R2 com o R2 predito. De maneira ideal, esses valores devem ser semelhantes. Um teste R2 que é significativamente menor do que o R2 predito indica que a validação cruzada é excessivamente otimista sobre a capacidade preditiva do modelo ou que as duas amostras de dados são de populações diferentes.
