Tabela Seleção e validação do modelo para Regressão de mínimos quadrados parciais

Os componentes representam o número de componentes incluídos em cada modelo. O Minitab exibe o modelo com 1 componente, com 2 componentes e assim por diante, até ele incluir o número de componentes que você especificou. Se você não tiver especificado o número de componentes a serem incluídos no modelo, o Minitab mostra as estatísticas da seleção do modelo para 10 componentes ou o número de preditoras, o que for menor.

A variância é a quantidade de variância nos termos que são explicados pelo modelo. O valor-x da variância está entre 0 e 1.

Quanto mais perto o valor-x da variância estiver de 1, os componentes representam melhor o conjunto original de termos. Se você tiver mais de 1 resposta, o valor-x da variância é o mesmo para todas as respostas.

O erro é a soma dos quadrados do erro, que é a soma dos resíduos quadrados. Ele quantifica a variação nos dados que o modelo não explica. Para o modelo final, o erro corresponde ao SQ do erro residual na tabela ANOVA do modelo final.

R² representa a porcentagem de variação na resposta que é explicada pelo modelo. Ele é calculado como 1 menos a razão da soma dos quadrados dos erros (que é a variação que não é explicada pelo modelo) para a soma total dos quadrados (que é a variação total no modelo).

Interpretação

Use R² para determinar se o modelo ajusta bem os dados. Quanto mais alto o valor de R² melhor o modelo ajusta seus dados. O valor de R² está sempre entre 0 e 100%.

Você pode usar um gráfico de linha ajustada para ilustrar graficamente valores de R² diferentes. O primeiro gráfico ilustra um modelo de regressão simples que explica 85,5% da variação na resposta. O segundo gráfico ilustra um modelo que explica 22,6% da variação na resposta. Quanto mais variação é explicada pelo modelo, mais perto os pontos de dados caem da linha de regressão ajustada. Teoricamente, se um modelo pudesse explicar 100% da variação, os valores ajustados sempre se igualariam aos valores observados e todos os pontos de dados cairiam sobre a linha ajustada. No entanto, mesmo se R² representar 100%, o modelo não necessariamente prediz bem as novas observações.

Considere as seguintes questões ao interpretar o valor de R²:

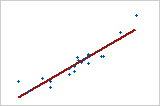
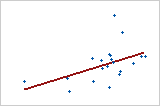
• O R² sempre aumenta quando você adiciona mais preditores a um modelo. Por exemplo, o melhor modelo de cinco preditores terá sempre um R² que é pelo menos tão elevado quanto o melhor modelo de quatro preditores. Portanto, R² é mais útil quando for comparado a modelos do mesmo tamanho.

• Amostras pequenas não fornecem uma estimativa precisa da força da relação entre a resposta e os preditores. Por exemplo, se você precisar que R² seja mais exato, deve usar uma amostra maior (geralmente, 40 ou mais).

• A estatística de qualidade do ajuste é apenas uma medida do grau em que o modelo ajusta os dados (se ajusta bem ou mal). Mesmo quando um modelo tem um um valor desejável, você deve verificar os gráficos de resíduos para conferir se o modelo atende aos pressupostos do modelo.

O R² predito indica em que grau cada modelo calculados prediz a resposta e somente é calculado quando você realiza uma validação cruzada. Se houver uma variável de resposta nos dados, o Minitab seleciona o modelo PLS com o R² predito mais alto. Se as variáveis de resposta estiverem nos dados, o Minitab seleciona o modelo PLS com o R² predito médio mais alto para todas as variáveis de resposta. O R² predito é calculado removendo-se sistematicamente cada observação do conjunto de dados, estimando a equação de regressão e determinando quão bem o modelo prediz a observação removida. O valor do R² predito varia entre 0% e 100%. (Enquanto os cálculos do R² predito podem produzir valores negativos, o Minitab exibe zero para esses casos).

A soma dos quadrados predita (PRESS) do erro é uma medida do desvio entre os valores ajustados e os valores observados. PRESS é semelhante à soma dos quadrados dos erros residuais (SSE), que é o somatório dos quadrados dos resíduos. No entanto, PRESS usa um cálculo diferente para os resíduos. A fórmula utilizada para calcular PRESS é equivalente a um processo para remover sistematicamente cada observação do conjunto de dados, estimando a equação de regressão, e determinando o quão bem o modelo prediz a observação removida.