Métodos e fórmulas para Regressão ortogonal

O modelo do erro de medição é:

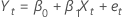
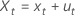
Na regressão ortogonal, a melhor linha de ajuste é aquela que minimiza as distâncias ortogonais ponderadas dos pontos traçados para a linha. Se a razão de variância de erro for 1, as distâncias ponderadas são distâncias euclidianas.

Notação

Termo	Descrição
Yt	resposta observada
β0	intercepto
β1	inclinação
Xt	preditora observada
xt	valor verdadeiro e não observado da preditora
et, ut	erros de medição; et, ut são independentes com média 0 e variâncias de erro de δe2 e δu2

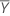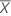Permita que a média da amostra seja (, ) e a matriz de covariância da amostra seja:

m_ZZ é uma matriz simétrica 2X2:

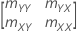
Notação

Termo	Descrição
Zt	(Yt, Xt)
n	tamanho da amostra

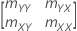
Se o elemento m_XY da matriz de covariância da amostra não é igual a 0, então:

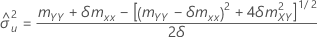
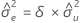
Se m_XY = 0 e m_YY < δm_XX,

Se m_XY = 0 e m_YY > δm_XX, as estimativas de parâmetro restantes são indefinidas.

Notação

Termo	Descrição
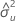	estimativa da variância de erro para X
	estimativa da variância de erro para Y
δ	razão de variâncias de erro
mXY	elemento da matriz de covariância da amostra
mYY	elemento da matriz de covariância da amostra
mXX	elemento da matriz de covariância da amostra

Se o elemento m_XY da matriz de covariância da amostra não é igual a 0, então:

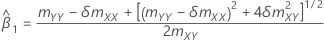
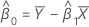
Se m_xy = 0 e m_yy < δm _xx','

Se m_xy = 0 e m_yy > δm_xx, as estimativas de parâmetro restantes são indefinidas.

Notação

Termo	Descrição
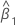	estimativa da inclinação
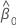	estimativa do intercepto
mxy	elemento da matriz de covariância da amostra
myy	elemento da matriz de covariância da amostra
δ	razão de variâncias de erro
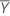	média de valores de resposta
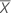	média de valores da preditora

Uma estimativa da matriz de covariância da distribuição aproximada do intercepto e da inclinação:

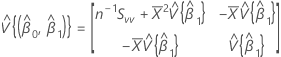
em que:

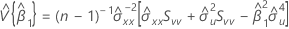
e

Se m_XY não for igual a 0:

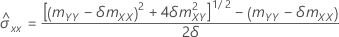
Se m_XY é igual a 0 e m_YY < δm_XX:

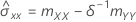
Notação

Termo	Descrição
	estimativa da inclinação
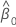	estimativa do intercepto
mXY	elemento da matriz de covariância da amostra
mYY	elemento da matriz de covariância da amostra
mXX	elemento da matriz de covariância da amostra
δ	razão de variâncias de erro
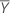	média de valores de resposta
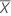	média de valores da preditora

O intervalo de confiança de 100(1 - α)% para β₀ é:

onde:

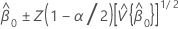
Z (1 - α / 2) é o percentil 100 * (1 - α / 2 ) para a distribuição normal padrão

e

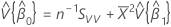, que é um elemento na matriz de covariância da distribuição aproximada

Notação

Termo	Descrição
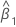	estimativa da inclinação
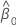	estimativa do intercepto
α	nível de significância

O intervalo de confiança de 100(1 - α)% para β₁ é:

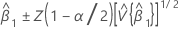
em que:

Z(1 - α / 2) é o percentil 100 * (1 - α / 2) da distribuição normal padrão

e

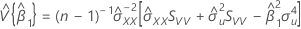
Notação

Termo	Descrição
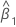	estimativa da inclinação
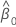	estimativa do intercepto
α	nível de significância

O valor ajustado da preditora x na regressão ortogonal é:

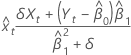
Notação

Termo	Descrição
δ	razão de variâncias de erro
Yt	tésimo valor de resposta
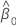	estimativa do intercepto
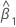	estimativa da inclinação

O valor ajustado para a resposta y na regressão ortogonal é:

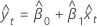
Notação

Termo	Descrição
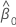	estimativa do intercepto
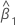	estimativa da inclinação
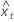	tésimo valor ajustado para x

O resíduo de uma observação na regressão ortogonal é:

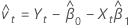
Notação

Termo	Descrição
Yt	tésimo valor de resposta
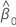	intercepto
Xt	tésimo valor da preditora
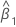	inclinação

O resíduo padronizado é útil na identificação de outliers. Ele é calculado como:

onde

Notação

Termo	Descrição
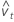	de resíduos
	desvio padrão do resíduo
δ	razão da variância do erro
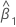	estimativa da inclinação
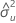	estimativa da variância de erro para X

A preditora de Y_{n + 1} é:

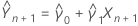
em que:

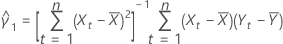
e

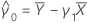
Notação

Termo	Descrição
Xt	tésimo valor da preditora
	média de valores da preditora
Yt	tésimo valor de resposta
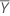	média de valores de resposta

em que:

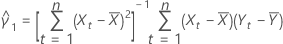
Notação

Termo	Descrição
myy	variância da amostra de Y
mxy	covariância da amostra entre as variáveis aleatórias X e Y