Neste tópico
Gráfico com linha ajustada
O gráfico com a linha ajustada mostra a resposta e os dados da preditora. O gráfico inclui a linha de regressão ortogonal, que representa a equação de regressão ortogonal.
Você também pode escolher exibir a linha ajustada de mínimos quadrados no gráfico para comparação. Grandes diferenças entre as duas linhas mostram quanto os resultados dependem se você se responsabiliza pela incerteza nos valores da variável preditora. Os valores de mínimos quadrados são iguais aos valores preditos para a regressão ortogonal, de forma que você também pode usar a linha de mínimos quadrados para examinar os valores preditos.
Interpretação
- A amostra contém um número adequado de observações em toda a amplitude de todos os valores da preditora.
- A amostra não contém nenhuma curvatura à qual o modelo não se ajusta.
- A amostra não contém nenhum outlier, o que pode ter um forte efeito nos resultados. Tente identificar a causa de qualquer outliers. Corrija todos os erros de entrada de dados ou erros distinguíveis de medição. Considere a remoção de valores de dados que estejam associados a eventos anormais que ocorrem somente uma vez (causas especiais). Em seguida, repita a análise.
Você geralmente usa a regressão ortogonal na química clínica ou em um laboratório para determinar se dois instrumentos ou métodos fornecem medições comparáveis.
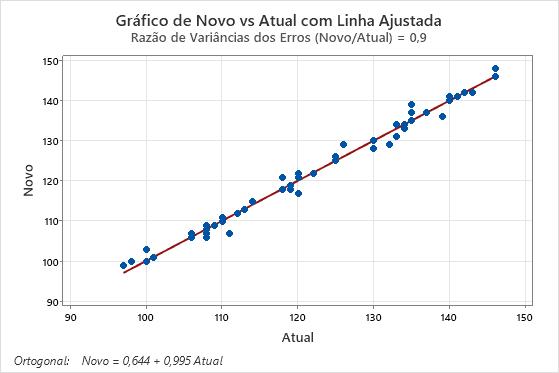
Este gráfico mostra um exemplo das medições de dois instrumentos ou métodos que são comparáveis. Os pontos seguem a linha ajustada com dispersão mínima e sem nenhum padrão que revele diferenças sistemáticas entre os métodos.
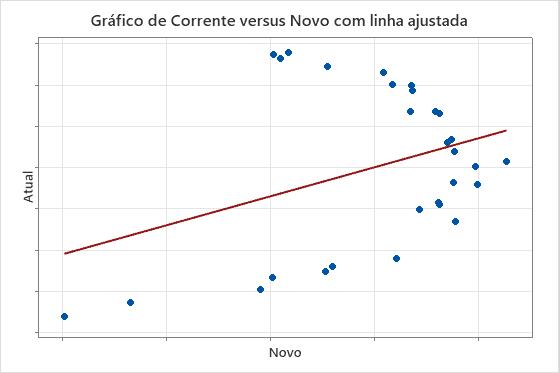
Nos resultados a seguir, os intervalos de confiança dos coeficientes não fornecem evidências de que as medições dos dois instrumentos diferem. Contudo, o gráfico mostra que os pontos não caem próximo à linha, o que indica que as medições dos dois instrumentos não são comparáveis. Como os dados não se ajustam à equação, a conclusão usual é que os instrumentos diferem.
Coeficientes
| Preditor | Coef. | EP de Coef | Z | P | IC de 95% Aprox. |
|---|---|---|---|---|---|
| Constante | -0,00000 | 0,215424 | -0,0000 | 1,000 | (-0,422224; 0,42222) |
| Nova | 1,00000 | 0,517586 | 1,9320 | 0,053 | (-0,014450; 2,01445) |
Histograma de resíduos
O histograma dos resíduos mostra a distribuição dos resíduos padronizados para todas as observações.
Interpretação
| Padrão | O que o padrão pode indicar |
|---|---|
| Uma longa cauda em uma direção | Assimetria |
| Uma barra que está longe das outras barras | Um outlier |
Você geralmente usa a regressão ortogonal na química clínica ou em um laboratório para determinar se dois instrumentos ou métodos medem a mesma coisa. Quando o modelo não atende às suposições, uma explicação é que os métodos não medem a mesma coisa.
Como a aparência de um histograma depende do número de intervalos usado para agrupar os dados, não use um histograma para avaliar a normalidade dos resíduos. Em vez disso, use um gráfico de probabilidade normal.
Um histograma é mais eficaz quando você tem aproximadamente 20 ou mais pontos de dados. Se a amostra é muito pequena, então cada barra no histograma não contém pontos de dados suficientes para confiavelmente mostrar assimetria ou outliers.
Gráficos de probabilidade normal de resíduos
Um gráfico de probabilidade normal dos resíduos mostra os resíduos versus seus valores esperados quando a distribuição é normal.
Interpretação
Use o gráfico de probabilidade normal de resíduos para verificar a pressuposição de que os resíduos são distribuídos normalmente. O gráfico de probabilidade normal dos resíduos deve seguir aproximadamente uma linha reta.
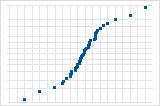
A curva S sugere uma distribuição com caudas longas.
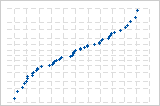
A curva S invertida sugere uma distribuição com caudas curtas.
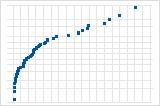
A curva descendente implica uma distribuição assimétrica à direita.
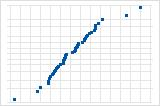
Alguns pontos situados longe da linha sugerem uma distribuição com outliers.
Você geralmente usa a regressão ortogonal na química clínica ou em um laboratório para determinar se dois instrumentos ou métodos medem a mesma coisa. Se você vê um padrão não normal, uma explicação é que os métodos não medem a mesma coisa. Além disso, os outros gráficos residuais para verificar outros problemas com o modelo, tais como efeito de ordem de tempo. Se os resíduos não seguirem uma distribuição normal, os intervalos de confiança e os valores-p podem ser inexatos.
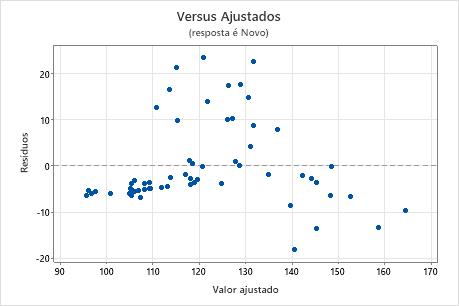
Resíduos versus ajustes
Os gráficos de resíduos versus ajustes representam os resíduos no eixo-y e os valores ajustados para a preditora no eixo-x.
Você geralmente usa a regressão ortogonal na química clínica ou em um laboratório para determinar se dois instrumentos ou métodos medem a mesma coisa. Quando o modelo não atende as suposições, uma explicação é que os métodos não medem a mesma coisa.
Interpretação
Use o gráfico de resíduos versus ajustes para verificar a pressuposição de que os resíduos são aleatoriamente distribuídos e têm variância constante. De maneira ideal, os pontos devem cair aleatoriamente em ambos os lados de 0, sem padrões reconhecíveis nos pontos.
| Padrão | O que o padrão pode indicar |
|---|---|
| Dispersão grande ou irregular de resíduos entre valores ajustados | Variância não constante |
| Curvilíneo | Um termo de ordem mais alta ausente |
| Um ponto que está distante de zero | Um outlier |
| Um ponto que é distante dos outros pontos na direção x | Um ponto influente |

Gráfico com outlier
Um dos pontos é muito maior do que todos os outros pontos. Portanto, a questão é um outlier. Se houver muitos outliers, o modelo pode não ser aceitável. Você deve tentar identificar a causa de todos os outliers. Corrija os erros de entrada de dados ou de medição. Considere a remoção de valores de dados que estejam associados a eventos anormais que ocorrem somente uma vez (causas especiais). Em seguida, repita a análise.
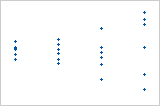
Gráfico com variância não constante
A variância dos resíduos aumenta com os valores ajustados. Observe que, como o valor dos ajustes aumenta, a dispersão entre os resíduos se torna mais ampla. Este padrão indica que as variâncias dos resíduos são desiguais (não constante).
Resíduos versus ordem
O gráfico de resíduos versus ordem mostra os resíduos na ordem em que os dados foram coletados.
Interpretação
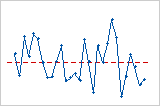
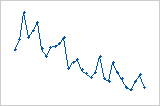
Tendência
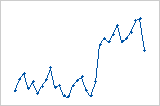
Deslocamento
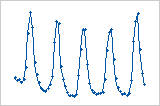
Ciclo
Resíduos versus as variáveis
O gráfico de resíduos versus variáveis apresenta os resíduos comparados com outras variáveis. A variável já pode estar incluída em seu modelo. Ou, a variável pode não estar no modelo, mas você suspeita que afeta a resposta.
Interpretação
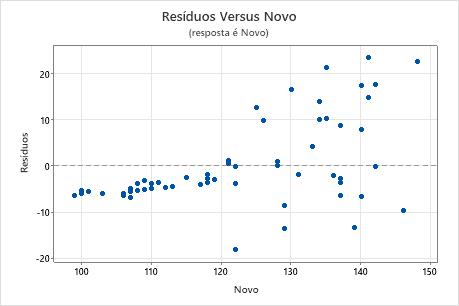
Você geralmente usa a regressão ortogonal na química clínica ou em um laboratório para determinar se dois instrumentos ou métodos medem a mesma coisa. Os padrões em um gráfico de resíduos contra a variável de resposta ou a variável da preditora podem esclarecer como um método é diferente do outro.
Nesses resultados, o gráfico de resíduos versus ajustes mostra um padrão onde todos os resíduos altos estão no meio do gráfico. Um gráfico dos resíduos versos a variável de resposta esclarece que como as leituras do novo método ficam maiores, o acordo com o outro método fica pior.