Selecione o método ou a fórmula de sua escolha.
Neste tópico
Restrições de parâmetro
Impor restrições de parâmetro transformando os parâmetros.1
| Se | Então |
|---|---|
| a < θ | θ = a + exp( φ ) |
| θ < b | θ = b - exp( φ ) |
| a < θ < b | θ = a +((b - a) / (1 + exp( -φ ))) |
| Termo | Descrição |
|---|---|
| a e b | constantes numéricas |
| De θ | parâmetros |
| φ | parâmetros transformados |
O Minitab realiza essas transformações e exibe os resultados em termos dos parâmetros originais.
- Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.
Erro padrão da estimativa de parâmetros
O erro padrão aproximado da estimativa de θp é o S vezes a raiz quadrada do elemento diagonal p de 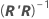 , que é escrito como:
, que é escrito como:

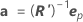

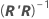 , que é escrito como:
, que é escrito como:

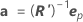

Notação
| Termo | Descrição |
|---|---|
| n | nésima observação |
| N | número de observações total |
| p | número de parâmetros livres (não bloqueados) |
| R | a matriz R (triangular superior) da decomposição de QR de Vi para a iteração final |
| V0 | matriz de gradiente = ( ∂f(xn, θ) / ∂θp), o P por 1 vetor de derivativos parciais de f(x0, θ), avaliado em θ* |
| S |
 |
Matriz de correlação das estimativas de parâmetro
A matriz de variância-covariância aproximada das estimativas de parâmetro é:
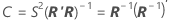
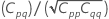

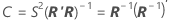
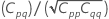

Notação
| Termo | Descrição |
|---|---|
| R | a matriz R (triangular superior) da decomposição de QR de Vi para a iteração final |
| P | número de parâmetros livres (não bloqueados) |
| v0 | matriz de gradiente = ( ∂f(xn, θ) / ∂θ p), o P por 1 vetor de derivativos parcial de f( x0, θ), avaliado em θ* |
| De θ | parâmetros |
Intervalos de confiança de probabilidade de perfil para parâmetros
Permita θ = (θ1, . . . . θp) * com θ* sendo a iteração final para θ.
Os limites de confiança baseados na probabilidade de 100 (1 - α) % satisfazem:
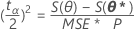
onde S( θp ) é o SSE obtido ao manter o θp fixo e minimizando sobre os outros parâmetros.1 Isso é equivalente à solução:
S(θp) = S(θ*) + (tα/2)2 MSE
Notação
| Termo | Descrição |
|---|---|
| De θ | parâmetros |
| n | nésima observação |
| N | número de observações total |
| P | número de parâmetros livres (não bloqueados) |
| tα/2 | ponto superior α/2 da distribuição t com N - P graus de liberdade |
| S(θ) | Soma do erro quadrado |
| MSE | erro quadrado médio |
- Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.
