Métodos em Regressão não-linear

A função de expectativa para observação n é denotada por:

O Minitab considera a função de expectativa para todas as N observações como uma função de valor de vetor dos parâmetros, conforme:

que é um vetor N X 1 com elementos .

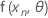
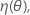
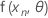O Jacobiano de η é uma matriz N X P com elementos que são iguais aos derivativos parciais da função de expectativa com respeito aos parâmetros:

Permita que Vⁱ = V(θⁱ) seja o Jacobiano avaliado em θⁱ, a estimativa de parâmetro após a iteração i.

Depois uma aproximação linear de η é:

que forma base para o método de Gauss-Newton e para inferências aproximadas.

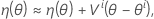
Permita que θ* denote a estimativa de mínimos quadrados.

Por padrão, o Minitab usa o método de Gauss-Newton para determinar a estimativa de mínimos quadrados. O método usa uma aproximação linear à função de expectativa para aprimorar iterativamente uma suposição inicial de θ⁰ para θ, e depois o método continua o aprimoramento das estimativas até que o offset relativo caia abaixo da tolerância prescrita¹. Isto é, o Minitab expande a função de expectativa f(x_n,θ) em uma série Taylor de primeira ordem sobre θ⁰ conforme:

em que

com p = 1, 2,..., p

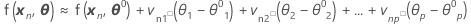
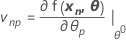
Incluindo todos os casos N

onde V⁰ é a matriz derivativa NxP com elementos {v_np}. Isso é equivalente a aproximar os resíduos, z(θ) = y - η(θ), em:

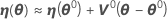
em que

e

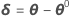
O Minitab calcula o incremento de Gauss δ⁰ para minimizar a soma aproximada dos quadrados dos resíduos 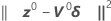, usando:

e assim por diante: .

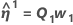
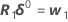O ponto

agora deve estar mais próximo de y do que de η(θ⁰), e o Minitab usa o valor θ¹ = θ⁰ + δ⁰ para realizar outra iteração ao calcular novos resíduos z¹ = y - η(θ¹), uma nova matriz derivativa V¹, e um novo incremento. O Minitab repete este processo até a convergência, que é quando o incremento é tão pequeno que não há mudança útil nos elementos do vetor do parâmetro.

Algumas vezes o incremento de Gauss-Newton produz um aumento na soma dos quadrados. Quando isso ocorre, a aproximação linear ainda é uma aproximação perto da superfície real para uma região pequena o suficiente ao redor de η(θ⁰). Para reduzir a soma dos quadrados, o Minitab introduz um fator etapa λ, e calcula:

O Minitab começa com λ = 1 e divide-a ao meio até que S(θ¹) < S( θ⁰).

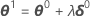
1. Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.

Quando as colunas em sua matriz de gradiente V têm colinearidade, ela pode tornar-se singular, causando comportamento errático de iterações de Gauss-Newton. Para lidar com a singularidade, o Minitab pode modificar o incremento de Gauss-Newton para o compromisso de Levenberg:

ou o compromisso de Marquardt:

onde k é um fator condicionante e D é uma matriz diagonal com entradas que são iguais aos elementos diagonais de V^TV. A direção de δ(k) é intermediária entre a direção do incremento de Gauss-Newton (k → 0) e a direção de descida mais íngreme:

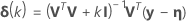
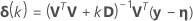
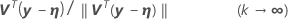.¹

1. Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.

Por padrão, o Minitab declara convergência quando o offset relativo é menor do que 1,0e-5. Isso assegura que quaisquer inferências não são afetadas materialmente pelo fato de que o vetor do parâmetro atual é menor que 0,001% do rádio do disco da região de confiança a partir do ponto de mínimos quadrados.¹

1. Bates and Watts (1988). Nonlinear Regression Analysis and Its Applications. John Wiley & Sons, Inc.