Neste tópico
Modelo
O Minitab calcula K – 1 funções de logit para um modelo com K categorias de resposta. Por exemplo, uma resposta com três categorias (1, 2, 3) tem duas funções de logit (evento de referência = 3):
Fórmula
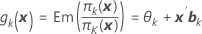
Notação
| Termo | Descrição |
|---|---|
| gk(x) | função de ligação do logit |
| θk | constante associada à késimacategoria de resposta distinta |
| xk | vetor das variáveis preditoras |
| bk | vetor dos coeficientes associados à késimafunção de logit |
Padrão de fator/covariável
Descreve um conjunto único de valores de fator/covariável em um conjunto de dados. O Minitab calcula probabilidades de evento, resíduos e outras medidas diagnósticas para cada padrão de fator/covariável.
Por exemplo, se um conjunto de dados inclui os fatores sexo e raça e a covariável idade, a combinação dessas preditoras pode conter tantos padrões de covariáveis diferentes quanto de indivíduos. Se um conjunto de dados só inclui os fatores raça e sexo, cada um codificado em dois níveis, só há quatro padrões de fator/covariáveis possíveis. Se você inserir seus dados como frequências, ou como sucessos, tentativas ou falhas, cada linha conterá um padrão de fator/covariável.
Probabilidade de evento
Denotado como π. Para um modelo de três categorias com as categorias 1, 2 e 3 (evento de referência 3), as probabilidades condicionais são:
Fórmula
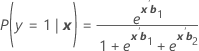
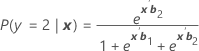
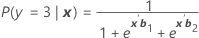
E a probabilidade do evento é:
πk(x) = P(y = k|x) para k = 1, 2, 3. Cada probabilidade é uma função do vetor de 2(p + 1) parâmetros, b' = (b'1, b'2)
Log-verossimilhança
A função log-verossimilhança é maximizada para gerar valores ótimos de b. Para um modelo com 3 categorias de resposta (referência = 3), a função log-verossimilhança é:
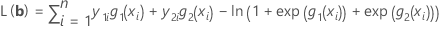
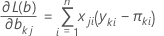
As estimativas de máxima verossimilhança são obtidas ajustando-se essas equações para zero e resolvendo para b.
Notação
| Termo | Descrição |
|---|---|
| k | 1, 2 |
| j | 0, 1, 2, ..., p |
| p | número de coeficientes no modelo, não incluindo os coeficientes da constante |
| πki | πk(xi), com x0i para cada assunto |
Coeficientes
As estimativas de máxima verossimilhança, também chamados de estimativas de parâmetro. Se houver K valores de resposta distintos, o Minitab estima K – 1 conjuntos de estimativas de parâmetro para cada preditora. Os efeitos variam de acordo com a categoria de resposta comparada ao evento de referência. Cada logit fornece as diferenças estimadas no log de chances de uma categoria de resposta versus o evento de referência. Os parâmetros nas equações K – 1 determinam parâmetros para logits usando todos os outros pares de categorias de resposta.
Os coeficientes estimados são calculados usando-se um método de mínimos quadrados reponderados iterativo, que é equivalente à estimativa de máxima verossimilhança.1,2
Referências
- D.W. Hosmer and S. Lemeshow (2000). Applied Logistic Regression. 2a. ed. John Wiley & Sons, Inc.
- P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Erro padrão de coeficientes
O erro padrão assintótico, que indica a precisão do coeficiente estimado. Quanto menor o erro padrão, mais precisa é a estimativa.
Consulte [1] e [2] para obter mais informações.
- A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
- P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Z
A estatística-Z usada para determinar se a preditora está significativamente relacionada à resposta. Valores absolutos maiores de Z indicam uma relação significativa. O valor-p indica on Z cai na distribuição normal.
Fórmula
Z = βi / erro padrão
A fórmula da constante é:
Z = θk / erro padrão
Para pequenas amostras, o teste de razão de verossimilhança pode ser um teste mais confiável de significância.
valor-p (P)
Usado nos testes de hipóteses para ajudá-lo a decidir se deve rejeitar ou não rejeitar uma hipótese nula. O valor-p é a probabilidade de se obter uma estatística de teste que seja pelo menos tão extrema quanto o valor calculado real, se a hipótese nula for verdadeira. Um valor cortado comumente usado para o valor-p é 0,05. Por exemplo, se o valor-p calculado de uma estatística de teste for menor do que 0,05, você rejeita a hipótese nula.
Razão de chances
Útil na interpretação da relação entre a preditora e a resposta.
A razão de chances (q) pode ser qualquer número não negativo. Uma razão de chances de 1 serve como a linha de base para comparação. Se θ = 1, não há associação entre a resposta e a preditora. Se θ > 1, as chances do evento de resposta da comparação são maiores para o nível de referência do fator (ou para níveis mais altos de uma preditora contínua). Se θ < 1, as chances do evento de resposta de comparação são menores para o nível de referência do fator (ou para níveis mais altos de uma preditora contínua). Os valores mais distantes de 1 representam graus mais fortes de associação.
Por exemplo, para um modelo com três categorias de resposta (1, 2, 3) e uma preditora, a razão de chances especifica as chances para a categoria de resultados k versus a categoria de resultados usada como evento de referência (neste exemplo, 3). A seguir encontra-se uma fórmula para a razão de chances de uma preditora com dois níveis, a e b.
Fórmula
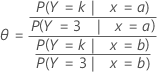
Notação
| Termo | Descrição |
|---|---|
| k | categoria de resultados |
Intervalo de confiança
Fórmula
O intervalo de confiança da amostra maior para βi é:
β i + Zα /2* (erro padrão)
Para obter o intervalo de confiança das razões de chances, exponencie os limites inferior e superior do intervalo de confiança. O intervalo fornece a amplitude no qual as chances podem se encaixar para cada mudança de unidade na preditora.
Notação
| Termo | Descrição |
|---|---|
| α | nível de significância |
Matriz de variância-covariância
Uma matriz quadrada com as dimensões p +1 × (K – 1). A variância de cada coeficiente está na célula diagonal e a covariância de cada par de coeficientes está na célula fora da diagonal apropriada. A variância é o erro padrão do coeficiente quadrado.
A matriz de variância-covariância é assintótica e é obtida da iteração final do inverso da matriz de informação. A matriz de segundos derivativos parciais é usada para obter a matriz de covariância.
Notação
| Termo | Descrição |
|---|---|
| p | número de preditoras |
| K | número de categorias na resposta |
Pearson
Uma estatística de resumo baseada nos resíduos de Pearson que indica quão bem o modelo se ajusta aos seus dados. A Pearson não é útil quando o número de valores distintos da covariável é aproximadamente igual ao número de observações, mas é útil quando você tem observações repetidas no mesmo nível das covariáveis. Valores maiores de estatísticas de teste χ2 e valores inferiores do valor-p indicam que o modelo pode não se ajustar bem aos dados.
A fórmula é:
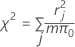
onde r = Pearson residual, m = número de ensaios no jésimo padrão de fator/covariável, e π0 = valor hipotético para a proporção.
Deviance
Um estatística de resumo baseada nos resíduos Deviance que indica quão bem o modelo se ajusta aos seus dados. O Deviance não é útil quando o número de valores distintos é aproximadamente igual ao número de observações, mas o teste é útil quando você tem observações repetidas no mesmo nível das covariáveis. Valores maiores de D e valores inferiores de valor-p indicam que o modelo pode não se ajustar bem aos dados. Os graus de liberdade para o teste é (k - 1)*J − (p) onde k é o número de categorias na resposta, J é o número de padrões de fator/covariável distintos e p é o número de coeficientes.
A fórmula é:
D =2 Σ yik log p ik− 2 Σ yik log π ik
onde πik = probabilidade da iésima observação para a késima categoria.
