Métodos e fórmulas para Gráfico de linha ajustada

Selecione o método ou a fórmula de sua escolha.

Neste tópico

Modelos de regressão polinomial
Coeficiente (Coef.)
S
R2
R2 (aj)
Graus de liberdade (DF)
Adj SS
MS Aj – Erro
MS Ajust – Regressão
Aj. de QM - Total
Valor-f
Valor-p – Tabela Análise de Variância
Resíduos (Resid)

Modelos de regressão polinomial

Fórmula

Você pode ajustar os seguintes modelos de regressão linear, quadrática ou cúbica:

Tipo do modelo	Pedido	Modelo estatístico
linear	primeiro	Y = β₀+ β₁x + e
quadrático	segundo	Y = β₀+ β₁x + β₂x²+ e
cúbico	terceiro	Y = β₀+ β₁x + β₂x²+ β₃x³+ e

Outra maneira de modelar a curvatura é gerar modelos adicionais usando o log 10 de x e/ou y para modelos linear, quadrático e cúbico. Além disso, adotando o log 10 de Y pode ser usado para reduzir a assimetria à direita ou variância não-constante de resíduos.

Quando o Minitab ajusta os modelos quadráticos ou cúbicos, o Minitab padroniza as preditoras antes de ela estimar os coeficientes. A padronização reduz a multicolinearidade entre as preditoras. A redução assegura que a multicolinearidade é tão baixa que não há probabilidade de o Minitab excluir nenhuma preditora do modelo. A saída mostra os coeficientes não padronizados nas unidades originais das preditoras."

Coeficiente (Coef.)

A fórmula para o coeficiente ou inclinação na regressão linear simples é:

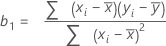
A fórmula para o intercepto (b₀) é:

Nos termos da matriz, a fórmula que calcula o vetor de coeficientes na regressão múltipla é:

b = (X'X)^-1X'y

Notação

Termo	Descrição
y_i	i^ésimo valor de resposta observado
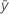	resposta média
x_i	i^ésimo valor da preditora
	preditora média
X	matriz de experimento
y	matriz de resposta

S

Notação

Termo	Descrição
MSE	quadrado médio do erro

R2

Outra apresentação da fórmula é:

R² também pode ser calculado como a correlação ao quadrado de y e .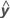

Notação

Termo	Descrição
SS	Soma dos Quadrados
y	variável de resposta
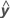	variável de resposta ajustada

R2 (aj)

Notação

Termo	Descrição
MS	Quadrado Médio
SS	Soma dos Quadrados
DF	Graus de liberdade

Graus de liberdade (DF)

Os graus de liberdade de cada componente do modelo são:

Fontes da variação	DF
Regressão	p
Erro	n – p – 1
Total	n – 1

Se os dados atendem a determinados critérios e o modelo inclui, no mínimo, uma preditora contínua ou mais de uma preditora categórica, o Minitab usa alguns graus de liberdade para o teste de falta de ajuste. Os critérios são os seguintes:

Os dados contêm múltiplas observações com os mesmos valores da preditora.
Os dados contêm os pontos corretos para estimar termos adicionais que não estão no modelo.

Notação

Termo	Descrição
n	número de observações
p	número de coeficientes no modelo, não contando a constante

Adj SS

A soma das distâncias quadradas. A regressão de SQ é a parte da variação explicada pelo modelo. O Erro da SQ é a parte não explicada pelo modelo e é atribuída ao erro. O Total da SQ é a variação total nos dados.

Fórmula

Regressão da SQ:

Erro da SQ:

Total da SQ:

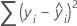
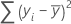
Notação

Termo	Descrição
y_i	i^ésimo valor de resposta observado
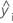	i^ésima resposta ajustada
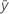	resposta média

MS Aj – Erro

O quadrado médio do erro (também abreviado como MS Erro ou MSE e denotado como s²) é a variação em torno da linha de regressão ajustada. A fórmula é:

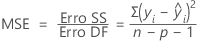
Notação

Termo	Descrição
y_i	i ^o valor de resposta observada
	i^a resposta ajustada
n	número de observações
p	número de coeficientes no modelo, sem contar com a constante

MS Ajust – Regressão

A fórmula para o Quadrado Médio (MS) da regressão é:

Notação

Termo	Descrição
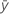	resposta média
	i^a resposta ajustada
p	o número de termos no modelo

Aj. de QM - Total

A fórmula para o total de Quadrados Médios (QM) é:

Notação

Termo	Descrição
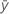	resposta média
y_i	i^ésimo valor de resposta observado
n	número de observações

Valor-f

As fórmulas para as estatísticas F são as seguintes:

(F (Regressão)
F(Termo)
F(Falta de ajuste)

Notação

Termo	Descrição
Regressão de QM	Uma medida da variação na resposta que o modelo atual explica.
Erro de QM	Uma medida da variação de que o modelo não explica.
Termo de QM	Uma medida da quantidade de variação que um termo explica após levar em conta os outros termos no modelo.
Falta de ajuste de QM	Uma medida da variação na resposta que poderia ser modelada adicionando-se mais termos ao modelo.
Erro puro de QM	Uma medida da variação em dados de resposta replicados.

Valor-p – Tabela Análise de Variância

O valor-p é a probabilidade que é calculada a partir de uma distribuição-f com graus de liberdade (DF) como a seguir:

DF do numerador: soma dos graus de liberdade para o termo ou os termos do teste
DF do denominador: graus de liberdade para erro

Fórmula

1 − P(F ≤ f_j)

Notação

Termo	Descrição
P(F ≤ f)	função de distribuição acumulada para a distribuição F
f	estatística F de teste

Resíduos (Resid)

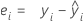
Notação

Termo	Descrição
e_i	i ^o resíduo
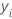	i ^o valor de resposta observada
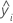	i ^a resposta ajustada