Um engenheiro de materiais em uma fábrica de móveis quer avaliar a dureza do aglomerado usado na fábrica. O engenheiro mede a rigidez e a densidade de uma amostra de peças de aglomerado.
O engenheiro usa regressão simples para determinar se a densidade das partículas está associada à rigidez da placa.
- Abra os dados amostrais, PlacaPartícula.MWX.
- Escolha .
- Em Resposta, digite Dureza.
- Em Preditor, digite Densidade.
- Em Tipo de Modelo de Regressão, selecione Quadrático.
- Clique em Gráficos. Em Gráficos de Resíduos, selecione Quatro em um. Clique em OK.
- Clique em Opções. Em Opções de Exibição, selecione Exibir intervalo de confiança e Exibir intervalo de predição.
- Clique em OK em cada caixa de diálogo.
Interprete os resultados
Na tabela Análise de Variância, o valor-p para o modelo de regressão é 0,000, o que significa que o valor-p atual é menor que 0,0005. Como o valor-p é menor que o nível de significância de 0,05, o engenheiro pode concluir que a associação entre dureza e densidade é estatisticamente significativa. Na tabela Análise de Variância Sequencial, o valor-p para o termo linear, Densidade é 0,000 e para o termo quadrático, Densidade2 é de 0,003. Ambos os valores são menores do que o nível de significância de 0,05.
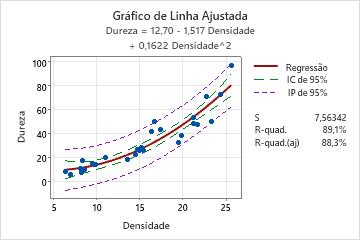
Contudo, parece haver um outlier no canto direito superior do gráfico de linha ajustada. Como o outlier poderia ter um forte efeito nos resultados, o engenheiro deve investigar este ponto para determinar sua causa.
Dureza = 12,70 - 1,517 Densidade + 0,1622 Densidade^2
Sumário do Modelo
| S | R2 | R2(aj) |
|---|---|---|
| 7,56342 | 89,13% | 88,29% |
Análise de Variância
| Fonte | GL | SQ | QM | F | P |
|---|---|---|---|---|---|
| Regressão | 2 | 12189,4 | 6094,70 | 106,54 | 0,000 |
| Erro | 26 | 1487,3 | 57,21 | ||
| Total | 28 | 13676,7 |
Análise de Variância Sequencial
| Fonte | GL | SQ | F | P |
|---|---|---|---|---|
| Linear | 1 | 11552,8 | 146,86 | 0,000 |
| Quadrático | 1 | 636,6 | 11,13 | 0,003 |