Neste tópico
Regressão ponderada
A regressão de mínimos quadrados ponderada é um método para lidar com as observações que têm variâncias não constantes. Se as variâncias são não constantes, observações com:
- grandes variâncias devem ser dadas em relação a pesos pequenos
- pequenas variâncias devem ser dadas em relação a pesos grandes
A escolha comum de pesos é o inverso da variância do erro puro na resposta.
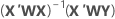
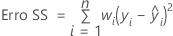
Notação
| Termo | Descrição |
|---|---|
| X | matriz do experimento |
| X' | transposição da matriz do experimento |
| W | uma matriz n x n com os pesos na diagonal |
| Y | vetor de valores de resposta |
| n | número de observações |
| wi | peso para a ia observação |
| yi | valor da resposta para a ia observação |
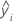 | valor ajustado para a ia observação |
Transformação Box-Cox
A transformação de Box-Cox seleciona valores de lambda, conforme mostrado a seguir, que minimizam a soma dos quadrados dos resíduos. A transformação resultante é Y λ quando λ ≠ 0 e ln(Y) quando λ = 0. Quando λ < 0, o Minitab também multiplica a resposta transformada por -1 para manter a ordem da resposta não transformada.
O Minitab pesquisa um valor ideal entre −2 e 2. Os valores que estão fora desse intervalo podem não resultar em um ajuste melhor.
A seguir estão algumas transformações comuns onde Y é a transformação dos dados Y:
| Valor lambda (λ) | Transformação |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0,5 | Y′ = 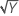 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0,5 |  |
| λ = −1 | Y′ = −1 / Y |
Equação de Regressão
Para um modelo com múltiplos preditores, a equação é:
y = β0 + β1x1 + ... + βkxk + ε
A equação ajustada é:
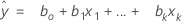
Na regressão linear simples, que inclui somente um preditor, o modelo é:
y=ß0+ ß1x1+ε
Usando estimativas de regressão b0 para ß0, e b1 para ß1, a equação ajustada é:
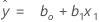
Equações com variável categórica
- Equação separada de cada conjunto de níveis de preditor categórico
- Equação única
- C1
- A variável resposta
- C2
- Um preditor contínuo
- C3
- Uma variável preditora categórica com os níveis Vermelho e Azul
- Azul: C1 = 0,184 + 0,1964*C2
- Vermelho: C1 = 0,011 + 0,1964*C2
Uma única equação usa uma variável indicadora para representar a variável categórica.
C1 = 0,184 + 0,1964*C2 + 0,0*C3_Azul- 0,173*C3_Vermelho
- Observação azul (C3_Azul = 1, C3_Vermelho = 0): C1 = 0,184 + 0,1964*C2 + 0,0*1 - 0,173*0 = 0,184 + 0,1964*C2
- Observação vermelha (C3_Azul = 0, C3_Vermelho = 1: C1 = 0,084 + 0,1964*C2 + 0,0*0 - 0,173*1 = 0,011 + 0,1964*C2
Notação
| Termo | Descrição |
|---|---|
| y | resposta |
| xk | Ok, no termo . Cada termo pode ser um único preditor, um termo polinomial ou um termo de interação. |
| ßk | késimo coeficiente de regressão populacional |
| ε | termo de erro que segue uma distribuição normal com uma média de 0 |
| bk | Estimativa do késimo coeficiente de regressão populacional |
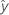 | resposta ajustada |
Matriz de experimento
A matriz de experimento contém as preditoras em uma matriz (X) com n setas, onde n é o número de observações. Há uma coluna para cada coeficiente no modelo.
As preditoras categóricas são codificadas usando-se as codificações 1, 0 ou -1, 0, 1. X não inclui uma coluna para o nível de referência do fator.
Para calcular as colunas para um termo de interação, multiplique todos os valores correspondentes para as preditoras na interação. Por exemplo, suponha que a primeira observação tenha um valor de 4 para a preditora A e um valor de 2 para a preditora B. Na matriz de experimento, a interação entre A e B está representada como 8 (4 x 2).
x'x inversa
Como o Minitab remove preditores fortemente correlacionados da equação de regressão no Ajuste do modelo de regressão
Seja rij o elemento na matriz de varredura atual associada a Xi e Xj.
As variáveis são inseridas ou removidas, uma de cada vez. Xk é elegível para entrada se for uma variável independente que não está atualmente no modelo com r kk ≥ 1 (tolerância com um padrão de 0,0001) e também para cada variável Xj que está atualmente no modelo,
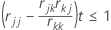
- O Minitab executa o método SWEEP na matriz de correlação, R, tratando X1 .. Xp como se fossem variáveis aleatórias.
- Para qualquer preditor contínuo, o Minitab compara o elemento rkk com a tolerância; rkk ≥ tolerância, onde k = 1 a p.
- Para cada variável Xj atualmente no modelo, o Minitab verifica que (rjj - rjk * (rkj / rkk))*tolerância ≤ 1.
Observação
Onde rkk, rjk, rjj são os elementos diagonais e off-diagonal correspondentes para as variáveis Xj e Xk após as operações k passo SWEEP.
- Caso contrário, o preditor falhará no teste e será removido do modelo.
Observação
O valor de tolerância padrão é 8.8e - 12.
Observação
Você pode usar o subcomando TOLERANCE com o comando de sessão REGRESS para forçar o Minitab a manter um preditor altamente correlacionado com outro preditor no modelo. Entretanto, diminuir a tolerância pode ser perigoso, e pode produzir resultados numericamente inexatos.
