Neste tópico
Ajuste
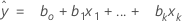
Notação
| Termo | Descrição |
|---|---|
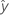 | valor ajustado |
| xk | ko termo. Cada termo pode ser um único preditor, um termo polinomial ou um termo de interação. |
| bk | estimativa do ko coeficiente de regressão |
Erro padrão do valor ajustado (EP Fit)
O erro padrão do valor ajustado em um modelo de regressão com um preditor é:

O erro padrão do valor ajustado em um modelo de regressão com mais de um preditor é:

Para regressão ponderada, inclua a matriz de peso na equação:

Quando os dados têm um conjunto de dados de teste ou validação cruzada k-fold, as fórmulas são as mesmas. O valor de s2 é dos dados de treinamento. A matriz de design e a matriz de peso também são dos dados de treinamento.
Notação
| Termo | Descrição |
|---|---|
| s2 | mean square error |
| n | number of observations |
| x0 | new value of the predictor |
 | mean of the predictor |
| xi | io predictor value |
| x0 | vector of values that produce the fitted values, one for each column in the design matrix, beginning with a 1 for the constant term |
| x'0 | transpose of the new vector of predictor values |
| X | design matrix |
| W | weight matrix |
Intervalo de confiança para um valor ajustado (IC)
Fórmula
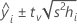
Para a regressão ponderada, a fórmula inclui os pesos:
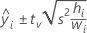
em que tv é o quantil 1-α/2 da distribuição t com v graus de liberdade para um intervalo bilateral. Para um limite unilateral, tv é o quantil 1-α da distribuição t com v graus de liberdade.
Quando você usa um conjunto de dados de teste ou validação cruzada de K dobras, os graus de liberdade e o quadrado médio do erro são do conjunto de dados de treinamento.
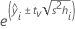
Notação
| Termo | Descrição |
|---|---|
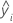 | fitted value |
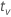 | quantile from the t distribution |
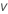 | degrees of freedom |
 | mean square error |
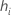 | leverage for the io observation |
| wi | weight for the io observation |
Resíduos
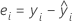
Notação
| Termo | Descrição |
|---|---|
| yi | iésimo valor de resposta observado |
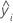 | iésimo valor ajustado para a resposta |
Resíduo padronizado (Std Resid)
Resíduos padronizados também são chamados de "resíduos estudentizados internamente".
Fórmula

Notação
| Termo | Descrição |
|---|---|
| ei | i o resíduo |
| hi | i o elemento diagonal de X(X'X)–1X' |
| s2 | quadrado médio do erro |
| X | matriz do experimento |
| X' | transposição da matriz do experimento |
Resíduos padronizados (Resíd Pad) com validação
Fórmula

Para regressão ponderada, a fórmula inclui o peso:
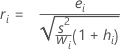
Notação
| Termo | Descrição |
|---|---|
| ei | io residual in the validation data set |
| hi | leverage for the io validation row |
| s2 | mean square error for the training data set |
| wi | weight for the io observation in the validation data set |
Resíduos (estudentizados) excluídos
Também chamados de resíduos estudentizados externamente. A fórmula é:
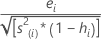
Outra apresentação desta fórmula é:

O modelo que estima a ia observação omite a ia observação do conjunto de dados. Portanto, a ia observação não pode influenciar a estimativa. Cada resíduo excluído tem distribuição t de Student com 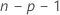 graus de liberdade.
graus de liberdade.
Notação
| Termo | Descrição |
|---|---|
| ei | iésimo residual |
| s(i)2 | erro de quadrado médio calculado sem a ia observação |
| hi | i ésimo elemento diagonal de X(X'X)–1X' |
| n | número de observações |
| p | número de termos, incluindo a constante |
| SSE | soma dos quadrados para erro |
