Neste tópico
Leverages (Hi)
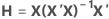
O leverage da ia observação é o io elemento diagonal, hi de H. Se hi for grande, a ia observação tem preditores incomuns (X1i, X2i, ..., Xpi). Isto é, os valores de predição estão longe da média do vetor 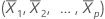 , usando a distância de Mahalanobis .
, usando a distância de Mahalanobis .
Os valores de leverage ficam entre 0 e 1. O Minitab identifica observações com leverages acima de 3p/n ou 0,99, o que for menor, com um X na tabela de observações incomuns. Normalmente, você examina valores com leverages grandes.
Notação
| Termo | Descrição |
|---|---|
| X | matriz de planejamento |
| hi | io elemento diagonal da matriz chapéu |
| p | número de termos no modelo incluindo a constante |
| n | número de observações |
Leverages (Hi) com validação
Fórmula

Para regressão ponderada, a fórmula inclui o peso:
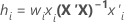
Notação
| Termo | Descrição |
|---|---|
| X | design matrix for the rows in the training data set or the folds that act as the training data set |
| xi | the vector of predictors in the io validation row |
| wi | weight for the io validation row |
Distância de Cook
A distância global, D, do impacto combinado entre todos os coeficientes de regressão estimados em uma observação. O Minitab calcula D usando valores de leverage e resíduos padronizados, e considera se uma observação é incomum no que se refere aos valores x e y. Observações com valores de D grandes podem ser outliers.
Fórmula
A distância de Cook é a distância entre os coeficientes calculados com e sem a i a observação. O Minitab calcula a distância de Cook sem ajustar uma nova equação de regressão cada vez que uma observação é omitida. Este cálculo é:

Notação
| Termo | Descrição |
|---|---|
| ei | i o resíduo |
| hi | i o elemento diagonal de 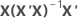 |
| p | número de parâmetros do modelo, incluindo a constante |
| s 2 | quadrado médio do erro |
| b | vetor do coeficiente |
| b(i) | vetor de coeficientes calculados depois de excluir a i a observação |
| X | matriz de planejamento |
DFITS
Combina valores de leverage e de resíduos estudentizados (resíduos t excluídos) em uma medida geral de como é uma observação incomum. DFITS mede a influência de cada observação sobre os valores ajustados em uma regressão e modelo ANOVA. Observações com valores de DFITS grandes podem ser outliers.
DFITS representa aproximadamente o número de desvios padrão que o valor ajustado muda quando cada observação é removida do conjunto de dados e o modelo é reajustado. O Minitab pode calcular o DFITS sem ajustar uma nova equação de regressão cada vez que uma observação é omitida.
Fórmula

Notação
| Termo | Descrição |
|---|---|
| ei | i o resíduo |
| hi | i o elemento diagonal de 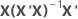 |
| X | matriz de planejamento |
 | i ésima resposta ajustada |
 | valor ajustado calculado sem a i a observação |
| MSE (i) | erro de quadrado médio calculado sem a i a observação |
| n | número de observações |
| p | número de parâmetros modelo |
Fator de inflação de variância (VIF)
O VIF pode ser obtido pela regressão de cada preditor sobre os preditores restantes e observando-se o valor de R2.
Fórmula
Para a preditora xj, o VIF é:

Notação
| Termo | Descrição |
|---|---|
| R2( xj) | coeficiente de determinação com xj como a variável de resposta e os outros termos no modelo como as preditoras |
Estatística de Durbin-Watson
Testes para a presença de autocorrelação nas residuais ao determinar se o não a correlação entre dois termos de erro adjacente é zero. O teste está baseado na suposição de que erros são gerados por um processo autorregressivo de primeira ordem. O Minitab supõe que as observações estão em uma ordem significativa, como ordem de tempo.

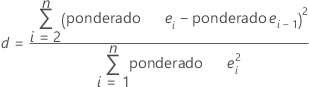
Notação
| Termo | Descrição |
|---|---|
| ei | io resíduo |
| ei -1 | residual para a observação anterior |
| n | número de observações |
