Selecione o método ou a fórmula de sua escolha.
Neste tópico
Coeficiente (Coef.)
A fórmula para o coeficiente ou inclinação na regressão linear simples é:
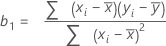
A fórmula para o intercepto (b0) é:

Nos termos da matriz, a fórmula que calcula o vetor de coeficientes na regressão múltipla é:
b = (X'X)-1X'y
Notação
| Termo | Descrição |
|---|---|
| yi | iésimo valor de resposta observado |
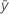 | resposta média |
| xi | iésimo valor da preditora |
 | preditora média |
| X | matriz de experimento |
| y | matriz de resposta |
Erro padrão do coeficiente (Coef. SE)
Para regressão linear simples, o erro padrão do coeficiente é:
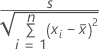
Os erros padrão dos coeficientes para regressão múltipla são as raízes quadradas dos elementos diagonais desta matriz:
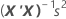
Notação
| Termo | Descrição |
|---|---|
| xi | iésimo valor da preditora |
 | média da preditora |
| X | matriz de experimento |
| X' | transposição da matriz de experimento |
| s2 | quadrado médio do erro |
Valor de T
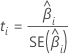
Notação
| Termo | Descrição |
|---|---|
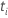 | estatística de teste para o  coeficiente coeficiente |
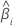 |  coeficiente estimado coeficiente estimado |
 | erro padrão de  coeficiente estimado coeficiente estimado |
Valor de p – Tabela Coeficientes
O valor de p bilateral para a hipótese nula de que um coeficiente de regressão é igual a 0 é:
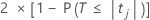
Os graus de liberdade são os graus de liberdade para erro, da seguinte forma:
n – p – 1
Notação
| Termo | Descrição |
|---|---|
 | A função distribuição acumulada da distribuição t com graus de liberdade iguais aos graus de liberdade para o erro. |
| tj | A estatística t para o jo coeficiente. |
| n | O número de observações no conjunto de dados. |
| p | A soma dos graus de liberdade para os termos. Os termos não incluem a constante. |
