Métodos e fórmulas para análise de variância em Ajuste do modelo de regressão

Selecione o método ou a fórmula de sua escolha.

Neste tópico

Soma de quadrados (SS)
Soma dos quadrados sequencial
Graus de liberdade (DF)
MS Ajust – Regressão
MS Aj – Erro
Aj. de QM - Total
Valor-f
Valor-p – Tabela Análise de Variância
Teste de ajuste (lack-of-fit) de erro puro
Valor-p – teste de ajuste (lack-of-fit)

Soma de quadrados (SS)

Nos termos da matriz, estas são as fórmulas para as diferentes somas dos quadrados:

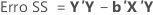
O Minitab decompõe o componente Tratamentos SS ou Regressão SS na quantidade de variação explicada por cada termo usando tanto a soma sequencial de quadrados como a soma ajustada de quadrados.

Notação

Termo	Descrição
b	vetor de coeficientes
X	matriz do experimento
Y	vetor de valores de resposta
n	número de observações
J	n por n matriz de 1s

Soma dos quadrados sequencial

O Minitab decompõe a o componente de Regressão SS ou Tratamentos da variância em somas dos quadrados sequenciais para cada fator. As somas dos quadrados sequenciais dependem da ordem dos fatores preditores e são inseridas no modelo. A soma dos quadrados sequencial é a parte única da Regressão SS explicada por um fator, considerando-se todos os fatores inseridos anteriormente.

Por exemplo, se você tem um modelo com três fatores ou preditores, X1, X2 e X3, a soma dos quadrados sequencial para X2 mostra quanto da variação restante é explicada por X2, considerando-se que X1 já está no modelo. Para obter uma sequência de fatores diferente, repita a análise e insira os elementos em uma ordem diferente.

Graus de liberdade (DF)

Os graus de liberdade de cada componente do modelo são:

Fontes da variação	DF
Regressão	p
Erro	n – p – 1
Total	n – 1

Se os dados atendem a determinados critérios e o modelo inclui, no mínimo, uma preditora contínua ou mais de uma preditora categórica, o Minitab usa alguns graus de liberdade para o teste de falta de ajuste. Os critérios são os seguintes:

Os dados contêm múltiplas observações com os mesmos valores da preditora.
Os dados contêm os pontos corretos para estimar termos adicionais que não estão no modelo.

Notação

Termo	Descrição
n	número de observações
p	número de coeficientes no modelo, não contando a constante

MS Ajust – Regressão

A fórmula para o Quadrado Médio (MS) da regressão é:

Notação

Termo	Descrição
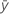	resposta média
	i^a resposta ajustada
p	o número de termos no modelo

MS Aj – Erro

O quadrado médio do erro (também abreviado como MS Erro ou MSE e denotado como s²) é a variação em torno da linha de regressão ajustada. A fórmula é:

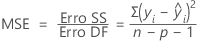
Notação

Termo	Descrição
y_i	i ^o valor de resposta observada
	i^a resposta ajustada
n	número de observações
p	número de coeficientes no modelo, sem contar com a constante

Aj. de QM - Total

A fórmula para o total de Quadrados Médios (QM) é:

Notação

Termo	Descrição
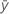	resposta média
y_i	i^ésimo valor de resposta observado
n	número de observações

Valor-f

As fórmulas para as estatísticas F são as seguintes:

(F (Regressão)
F(Termo)
F(Falta de ajuste)

Notação

Termo	Descrição
Regressão de QM	Uma medida da variação na resposta que o modelo atual explica.
Erro de QM	Uma medida da variação de que o modelo não explica.
Termo de QM	Uma medida da quantidade de variação que um termo explica após levar em conta os outros termos no modelo.
Falta de ajuste de QM	Uma medida da variação na resposta que poderia ser modelada adicionando-se mais termos ao modelo.
Erro puro de QM	Uma medida da variação em dados de resposta replicados.

Valor-p – Tabela Análise de Variância

O valor-p é a probabilidade que é calculada a partir de uma distribuição-f com graus de liberdade (DF) como a seguir:

DF do numerador: soma dos graus de liberdade para o termo ou os termos do teste
DF do denominador: graus de liberdade para erro

Fórmula

1 − P(F ≤ f_j)

Notação

Termo	Descrição
P(F ≤ f)	função de distribuição acumulada para a distribuição F
f	estatística F de teste

Teste de ajuste (lack-of-fit) de erro puro

Para calcular o teste de ajuste (lack-of-fit) de erro puro, o Minitab calcula:

A soma dos desvios quadrados da resposta da média dentro de cada conjunto de replicações adiciona-os juntos para criar a soma dos quadrados do erro puro (SS PE).
O quadrado médio do erro puro

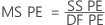
onde n = número de observações e m = número de combinações de nível x distintas
A soma dos quadrados do teste de ajuste (lack-of-fit)
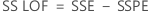
O quadrado médio do teste de ajuste (lack-of-fit)
A estatística de teste

Valores de F altos e valores de p baixos sugerem que o modelo é inadequado.

Valor-p – teste de ajuste (lack-of-fit)

Este valor-p é para o teste da hipótese nula de que os coeficientes são 0 por quaisquer termos que sejam possíveis de serem estimados a partir destes dados que não estão no modelo. O valor-p é a probabilidade de uma distribuição F com graus de liberdade (DF) como a seguir:

DF do numerador: graus de liberdade do teste de ajuste (lack-of-fit)
DF do denominador: graus de liberdade para erro puro

Fórmula

1 − P(F ≤ f_j)

Notação

Termo	Descrição
P(F ≤ f_j)	função de distribuição acumulada para a distribuição F
f_j	estatística F de teste