Neste tópico
Coeficientes
[1] P. McCullagh and J. A. Nelder (1989). Generalized Linear Models, 2a. Ed., Chapman & Hall/CRC, Londres.
Erro padrão de coeficientes
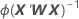
W é uma matriz diagonal onde os elementos diagonais são dados pela seguinte fórmula:
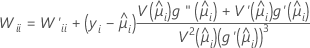
onde

Esta matriz de variância-covariância está baseada na matriz Hessiana observada em oposição à matriz de informação de Fisher. O Minitab usa a matriz Hessiana observada porque o modelo que resulta é mais robusto contra qualquer especificação incorreta média condicional.
Se a ligação canônica for usada, a matriz Hessiana observada e a matriz de informações de Fisher são idênticas.
Notação
| Termo | Descrição |
|---|---|
| yi | o valor de resposta da iésima linha |
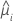 | a resposta média estimada da iésima linha |
| V(·) | a função de variância dada na tabela a seguir |
| g(·) | a função de ligação |
| V '(·) | o primeiro derivativo da função de variância |
| g'(·) | o primeiro derivativo da função de ligação |
| g''(·) | o segundo derivativo da função de ligação |
A função de variância depende do modelo:
| Modelo | Função de variância |
| Binomial | 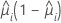 |
| Poisson | 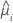 |
Consulte [1] e [2] para obter mais informações.
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
Z
A estatística-Z usada para determinar se a preditora está significativamente relacionada à resposta. Valores absolutos maiores de Z indicam uma relação significativa. A fórmula é:
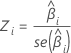
Notação
| Termo | Descrição |
|---|---|
| Zi | A estatística de teste para uma distribuição normal padrão |
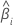 | O coeficiente estimado |
 | O erro padrão do coeficiente estimado |
Para pequenas amostras, o teste de razão de verossimilhança pode ser um teste mais confiável de significância. Os valores-p da razão de verossimilhança estão na tabela deviance. Quando o tamanho amostral é grande o bastante, os valores-p das estatísticas Z aproximam os valores-p das estatísticas da razão de verossimilhança.
valor-p (P)
Usado nos testes de hipóteses para ajudá-lo a decidir se deve rejeitar ou não rejeitar uma hipótese nula. O valor-p é a probabilidade de se obter uma estatística de teste que seja pelo menos tão extrema quanto o valor calculado real, se a hipótese nula for verdadeira. Um valor cortado comumente usado para o valor-p é 0,05. Por exemplo, se o valor-p calculado de uma estatística de teste for menor do que 0,05, você rejeita a hipótese nula.
Intervalo de confiança
O grande intervalo de confiança da amostra de um coeficiente estimado é:
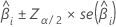
Para regressão logística binária, o Minitab fornece intervalos de confiança para as razões de chances. Para obter o intervalo de confiança das razões de chances, exponencie os limites inferior e superior do intervalo de confiança. O intervalo fornece o intervalo no qual as chances podem se encaixar para mudança de unidade na preditora.
Notação
| Termo | Descrição |
|---|---|
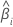 | o iésimo coeficiente |
 | a probabilidade acumulada inversa da distribuição normal padrão em 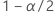 |
 | o nível de significância |
 | o erro padrão do coeficiente estimado |
Matriz de variância-covariância
Uma matriz d x d, onde d é o número de preditoras mais um. A variância de cada coeficiente está na célula diagonal e a covariância de cada par de coeficientes está na célula fora da diagonal apropriada. A variância é o erro padrão do coeficiente quadrado.
A matriz de variância-covariância é da iteração final do inverso da matriz de informação. A matriz de variância-covariância tem a seguinte forma:
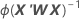
W é uma matriz diagonal onde os elementos diagonais são dados pela seguinte fórmula:

onde

Esta matriz de variância-covariância está baseada na matriz Hessiana observada em oposição à matriz de informação de Fisher. O Minitab usa a matriz Hessiana observada porque o modelo que resulta é mais robusto contra qualquer especificação incorreta média condicional.
Se a ligação canônica for usada, a matriz Hessiana observada e a matriz de informações de Fisher são idênticas.
Notação
| Termo | Descrição |
|---|---|
| yi | o valor de resposta da iésima linha |
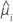 | a resposta média estimada da iésima linha |
| V(·) | a função de variância dada na tabela a seguir |
| g(·) | a função de ligação♣ |
| V '(·) | o primeiro derivativo da função de variância |
| g'(·) | o primeiro derivativo da função de ligação |
| g''(·) | o segundo derivativo da função de ligação |
A função de variância depende do modelo:
| Modelo | Função de variância |
| Binomial | 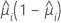 |
| Poisson | 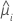 |
Consulte [1] e [2] para obter mais informações.
[1] A. Agresti (1990). Categorical Data Analysis. John Wiley & Sons, Inc.
[2] P. McCullagh and J.A. Nelder (1992). Generalized Linear Model. Chapman & Hall.
