Neste tópico
Gráfico de linha ajustada binária
O gráfico de linha ajustada exibe os dados de resposta e preditores. O gráfico inclui a linha de regressão, que representa a equação de regressão. Também é possível optar por exibir o intervalo de confiança para os valores ajustados.
Interpretação
Use o gráfico de linha ajustada para examinar a relação entre a variável de resposta e a variável de predição.
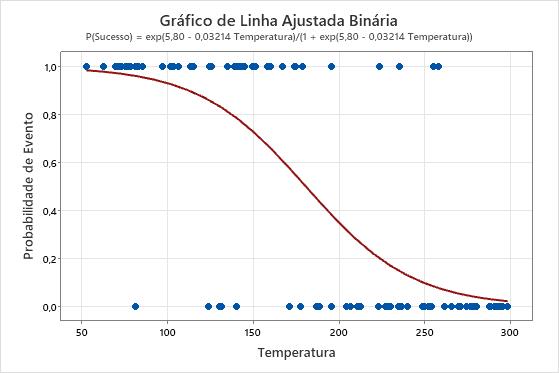
Nestes resultados, a equação é escrita como a probabilidade de um sucesso. O valor de resposta de 1 no eixo y representa um sucesso. O gráfico mostra que a probabilidade de um sucesso diminui à medida que a temperatura aumenta. Quando as temperaturas nos dados estão perto de 50, a inclinação da linha não é muito acentuada, o que indica que a probabilidade diminui lentamente à medida que a temperatura aumenta. A linha é mais acentuado na porção média dos dados de temperatura, o que indica que uma mudança na temperatura de 1 grau exerce maior efeito sobre essa faixa. Quando a probabilidade de um sucesso se aproxima de zero na extremidade superior do intervalo de temperatura, a linha achata novamente.
Se o modelo ajusta bem os dados, as probabilidades com alta predição mostram onde o evento é comum. Quando as temperaturas nos dados estão perto de 50, o valor de resposta de 1 é o mais comum. Conforme a temperatura aumenta, o valor de resposta de zero torna-se mais comum.
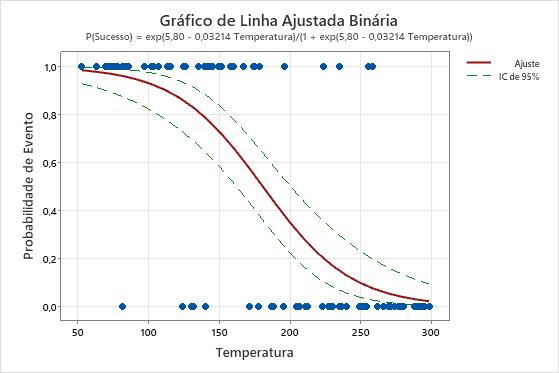
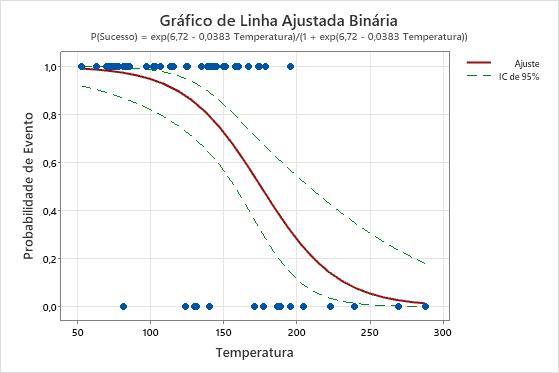
Se você adicionar intervalos de confiança ao gráfico, poderá usar os intervalos para avaliar quão precisas são as estimativas dos valores ajustados. No primeiro gráfico a seguir, as linhas do intervalo de confiança são aproximadamente da mesma largura que conforme a preditora aumenta. No segundo gráfico, o intervalo de confiança fica mais amplo conforme o valor da preditora aumenta. O intervalo mais amplo é parcialmente devido à pequena quantidade de dados, quando a temperatura é alta.
Histograma de resíduos
O histograma dos resíduos de deviance mostra a distribuição dos resíduos para todas as observações.
Interpretação
| Padrão | O que o padrão pode indicar |
|---|---|
| Uma longa cauda em uma direção | Assimetria |
| Uma barra que está longe das outras barras | Um outlier |
Como a aparência de um histograma depende do número de intervalos usado para agrupar os dados, não use um histograma para avaliar a normalidade dos resíduos. Em vez disso, use um gráfico de probabilidade normal.
Gráficos de probabilidade normal de resíduos
Um gráfico de probabilidade normal dos resíduos mostra os resíduos versus seus valores esperados quando a distribuição é normal.
Interpretação
Use o gráfico de probabilidade normal de resíduos para verificar a pressuposição de que os resíduos são distribuídos normalmente. O gráfico de probabilidade normal dos resíduos deve seguir aproximadamente uma linha reta.
A curva S sugere uma distribuição com caudas longas.
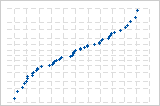
A curva S invertida sugere uma distribuição com caudas curtas.
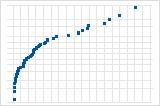
A curva descendente implica uma distribuição assimétrica à direita.
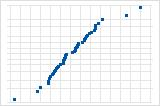
Alguns pontos situados longe da linha sugerem uma distribuição com outliers.
Se você vir um padrão não-normal, use os outros gráficos de resíduos para verificar outros problemas com o modelo, como termos faltantes ou um efeito de ordem de tempo. Se os resíduos não seguirem uma distribuição normal, os intervalos de confiança de aproximação normal e os valores-p do teste de Wald podem ser inexatos.
Resíduos versus ajustes
O gráfico de resíduos versus ajustes representa graficamente os resíduos no eixo Y e os valores ajustados no eixo X. O gráfico é significativo quando os dados estão no formato de Evento/Ensaio. Quando os dados estão no formato de Resposta/Frequência binária, o Minitab não fornece esse gráfico.
Interpretação
Use o gráfico de resíduos versus ajustes para verificar a pressuposição de que os resíduos são aleatoriamente distribuídos. De maneira ideal, os pontos devem cair aleatoriamente em ambos os lados de 0, sem padrões reconhecíveis nos pontos.
| Padrão | O que o padrão pode indicar |
|---|---|
| Dispersão grande ou irregular de resíduos entre valores ajustados | Uma função de link inadequada |
| Curvilíneo | Um termo de ordem superior faltante ou uma função de link inadequada |
| Um ponto que está distante de zero | Um outlier |
| Um ponto que é distante dos outros pontos na direção x | Um ponto influente |

Gráfico com outlier
Um dos pontos é muito maior do que todos os outros pontos. Portanto, a questão é um outlier. Se houver muitos outliers, o modelo pode não ser aceitável. Você deve tentar identificar a causa de todos os outliers. Corrija os erros de entrada de dados ou de medição. Considere a remoção de valores de dados que estejam associados a eventos anormais que ocorrem somente uma vez (causas especiais). Em seguida, repita a análise.
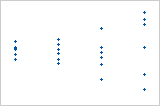
Gráfico com variância não constante
A variância dos resíduos aumenta com os valores ajustados. Observe que, como o valor dos ajustes aumenta, a dispersão entre os resíduos se torna mais ampla. Este padrão indica que as variâncias dos resíduos são desiguais (não constante).
| Problema | Solução possível |
|---|---|
| Variância não constante | Considere o uso de termos diferentes no modelo, uma função de link diferente ou pesos. |
| Um outlier ou ponto influente |
|
Resíduos versus ordem
O gráfico de resíduos versus ordem mostra os resíduos na ordem em que os dados foram coletados.
Interpretação
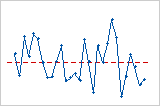
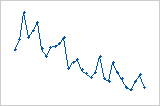
Tendência
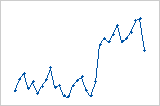
Deslocamento
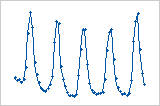
Ciclo
Resíduos versus variáveis
O gráfico de resíduos versus variáveis apresenta os resíduos comparados com outras variáveis. A variável já pode estar incluída em seu modelo. Ou, a variável pode não estar no modelo, mas você suspeita que afeta a resposta.
Interpretação
Se você observar um padrão não aleatória nos resíduos, isso indica que a variável afeta a resposta de uma forma sistemática. Considere a inclusão desta variável em uma análise.
