Métodos para Ajuste de modelo e Descubrir preditores-chave com Regressão TreeNet^®

Observação

Este comando está disponível com o Módulo de análise preditiva. Clique aqui saber mais sobre como ativar o módulo.

Os modelos do TreeNet^® representam uma abordagem para resolver problemas de classificação e regressão que são mais precisos e resistentes ao sobreajuste do que uma única classificação ou árvore de regressão. Uma descrição ampla e geral do processo é o que começamos com uma árvore de regressão pequena como modelo inicial. Dessa árvore vêm resíduos para cada linha nos dados que se tornam a variável de resposta para a próxima árvore de regressão. Criamos outra pequena árvore de regressão para predizer os resíduos da primeira árvore e calcular os resíduos resultantes novamente. Repetimos esta sequência até que um número ótimo de árvores com erro mínimo de predição seja identificado usando um método de validação. A sequência resultante de árvores forma o Modelo de regressão TreeNet^®.

Para o caso de regressão, podemos adicionar uma descrição geral da análise, mas alguns detalhes dependem de qual dos seguintes é a função de perda:

^^^Table : 1. Valores para a função de perda de erro quadrado
Estatística	Valor
Ajuste inicial,	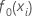média da variável de resposta
Resíduos generalizados, 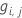como valor de resposta para a linha i
Dentro de atualizações de nó,	média de

^^^Table : 2. Valores para a função de perda de desvio absoluto
Estatística	Valor
Ajuste inicial,	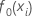mediana da variável resposta
Resíduos generalizados, 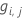como valor de resposta para a linha i
Dentro de atualizações de nó,	mediana de

Função de perda de Huber

Para a função de perda Huber, as estatísticas são as seguintes:

O ajuste inicial, 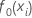, iguala a mediana de todos os valores de resposta.

Para cultivar a j-ésima árvore,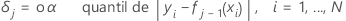

Em seguida, o resíduo generalizado para a i-ésima linha é o seguinte:

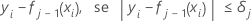
Os resíduos generalizados são usados como valores de resposta para cultivar a j-ésima árvore.

O valor atualizado para linhas no nó do m-ésimo terminal da j-ésima árvore é o seguinte:

Definir

para ser o residual regular para a i-ésima linha depois que j-1 árvores são cultivadas. Seja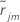

a mediana de

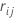valores para linhas dentro do nó terminal m da j-ésima árvore. Em seguida, o valor atualizado para cada linha dentro do m-ésimo nó de terminal da j-ésima árvore é:

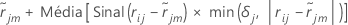
A média na expressão anterior é calculada em todas as linhas dentro do nó terminal m da j-ésima árvore.

Notação para funções de perda

Nos detalhes anteriores, 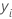é o valor da variável de resposta para a linha i, é o valor ajustado das j – 1 árvores anteriores, e 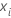é um vetor que representa a i^-ésima linha dos valores preditores nos dados de treinamento.

Parâmetros de entrada

A criação do modelo também utiliza as seguintes entradas do analista:

Entrada	Símbolo
taxa de aprendizado
taxa amostral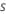
número máximo de nós terminais por árvore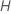
número de árvores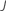
valor de comutação

Processo geral

O processo tem as seguintes etapas gerais para o cultivo da j-ésima, árvore, j=1,…,J:

Desenhe uma amostra aleatória de tamanho s * N dos dados de treinamento, em que N é o número de linhas nos dados de treinamento.
Calcule os resíduos generalizados, 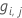, para .
Ajuste uma árvore de regressão com no máximo M nós terminais aos resíduos generalizados. A árvore divide as observações em no máximo m grupos mutuamente exclusivos.
Para o nó do m-ésimo terminal na árvore de regressão, calcule as atualizações dentro do nó na árvore que dependem da função de perda, .
Reduza as atualizações de dentro do nó de acordo com a taxa de aprendizagem e aplique os valores para obter os valores ajustados atualizados, :
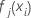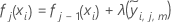
Repita as etapas 1-5 para cada árvore J na análise.