Observação
Este comando está disponível com o Módulo de análise preditiva. Clique aqui saber mais sobre como ativar o módulo.
Uma equipe de pesquisadores quer usar dados de um processo de moldagem por injeção para estudar configurações para máquinas que maximizam um tipo de força de uma peça plástica. As variáveis incluem controles nas máquinas, diferentes fórmulas plásticas e máquinas de moldagem por injeção.
Como parte da exploração inicial dos dados, a equipe decide usar Descubrir preditores-chave para comparar modelos removendo sequencialmente preditores sem importância para identificar preditores-chave. Os pesquisadores esperam identificar os principais preditores que têm mais efeito na resposta e obter mais informações sobre as relações entre a resposta e os principais preditores.
- Abra o conjunto de dados de amostra processo_de_injeção.MWX.
- Selecione .
- Em Resposta, digite força.
- Em Preditores contínuos, digite 'pressão de injeção' – 'Temperatura em medição'.
- Em Preditores categóricos, insira máquina e fórmula.
- Clique em OK.
Interpretar os resultados
Para esta análise, o Minitab Statistical Software compara 20 modelos. O asterisco na coluna Modelo da tabela de avaliação de modelos mostra que o modelo com maior valor da estatística R2 validada cruzada é o modelo 16. O modelo 16 contém 5 preditores importantes. Os resultados que seguem a tabela de avaliação do modelo são para o modelo 16.
Embora o Modelo 16 tenha o maior valor da estatística R2 validada cruzada, outros modelos possuem valores semelhantes. A equipe pode clicar em Selecione o modelo alternativo para produzir resultados para outros modelos da tabela de avaliação de modelos.
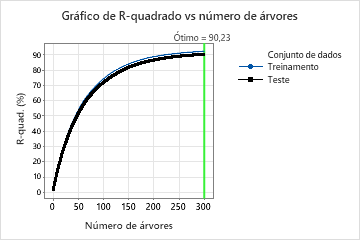
Nos resultados do modelo 16, o Gráfico R-quadrado versus número de árvores mostra que o número ótimo de árvores é igual ao número de árvores na análise, 300. A equipe pode clicar em Ajustar hiperparâmetros para aumentar o número de árvores e para ver se mudanças em outros hiperparâmetros melhoram o desempenho do modelo.
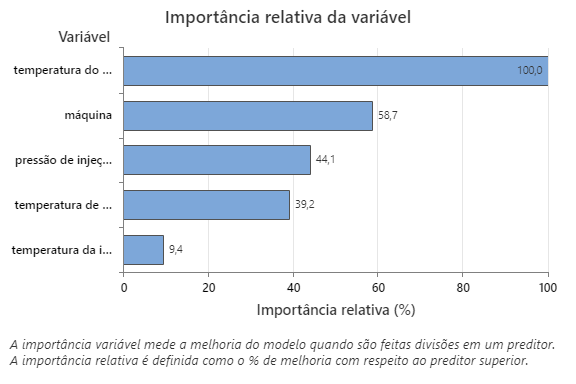
O gráfico de importância relativa da variável representa os preditores por ordem de seu efeito sobre a melhoria do modelo quando as divisões são feitas em um preditor sobre a sequência de árvores. A variável preditora mais importante é Temperatura do molde. Se a importância da variável principal do preditor, Temperatura do molde, for 100%, a próxima variável importante, Máquina, terá uma contribuição de 58,7%. Isso significa que a máquina que injeta é 58,7% tão importante quanto a temperatura no interior do molde.
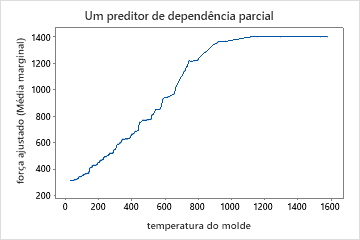
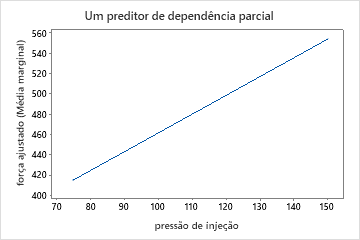
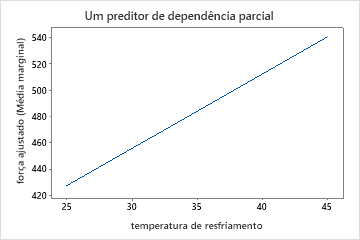
Use os gráficos de dependência parcial para obter uma visão de como as variáveis importantes ou pares de variáveis afetam a resposta predita. Os gráficos de dependência parcial mostram se a relação entre a resposta e uma variável é linear, monotônica ou mais complexa.
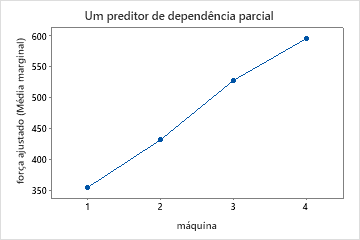
Os gráficos de dependência parcial do preditor mostram que a temperatura do molde, a pressão de injeção e a temperatura de resfriamento têm uma relação positiva com força. O gráfico das máquinas mostra as diferenças entre as máquinas, com a máquina 1 fazendo as peças mais fracas em média e a máquina 4 fazendo as peças mais fortes em média. A equipe nota que a temperatura do molde e a máquina têm a interação mais forte nos dados, então eles olham para o gráfico de dependência parcial de dois preditores para entender melhor como essas variáveis afetam a força. A equipe pode selecionar os resultados para produzir gráficos para outras variáveis, como a temperatura de injeção.
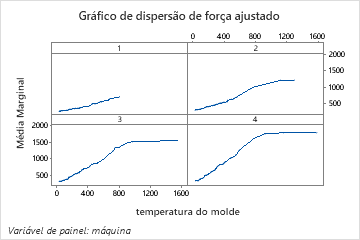
O gráfico de dependência parcial de dois preditores de Temperatura do molde e Máquina dá algumas informações sobre os pontos fortes médios da diferença para as máquinas. Uma das razões é que os dados da máquina 1 não incluem tantas observações nas temperaturas mais altas do molde quanto as outras máquinas. A equipe ainda poderia decidir procurar outras razões para que as máquinas produzam diferentes pontos fortes quando outras configurações são as mesmas. A equipe pode clicar nos resultados para produzir gráficos para outros pares de variáveis.
Método
| Função de perda | Erro quadrado |
|---|---|
| Critério para seleção do número ótimo de árvores | R-quadrado máximo |
| Validação do modelo | Validação cruzada de 3 dobras |
| Taxa de aprendizado | 0,01408 |
| Fração da subamostra | 0,5 |
| Nós máximos terminais por árvore | 6 |
| Tamanho mínimo do nó terminal | 3 |
| Número de preditores selecionados para divisão de nós | Número total de preditores = 21 |
| Linhas usadas | 1408 |
Informações da Resposta
| Média | DesvPad | Mínimo | Q1 | Mediana | Q3 | Máximo |
|---|---|---|---|---|---|---|
| 485,247 | 318,611 | 41,2082 | 301,099 | 398,924 | 562,449 | 2569,04 |
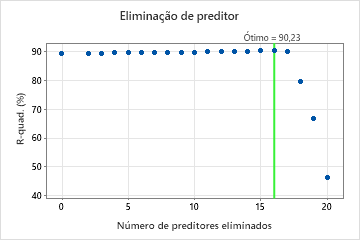
Seleção do modelo pela eliminação de preditores sem importância
| Modelo | Número ótimo de árvores | R-quadrado (%) | Número de preditores | Preditores eliminados |
|---|---|---|---|---|
| 1 | 300 | 89,32 | 21 | Nenhum |
| 2 | 300 | 89,34 | 19 | Taxa de fluxo de plástico; mudar de posição |
| 3 | 300 | 89,39 | 18 | temperatura de secagem |
| 4 | 300 | 89,46 | 17 | Zona de temperatura derretida 2 |
| 5 | 300 | 89,51 | 16 | Temperatura plástica |
| 6 | 300 | 89,50 | 15 | fórmula |
| 7 | 300 | 89,59 | 14 | Segurar pressão |
| 8 | 300 | 89,57 | 13 | almofada para parafusos |
| 9 | 300 | 89,69 | 12 | Zona de temperatura derretida 4 |
| 10 | 300 | 89,70 | 11 | pressão nas costas |
| 11 | 300 | 89,86 | 10 | Zona de temperatura derretida 1 |
| 12 | 300 | 89,90 | 9 | tempo de secagem |
| 13 | 300 | 89,92 | 8 | Temperatura em medição |
| 14 | 300 | 90,06 | 7 | Zona de temperatura derretida 5 |
| 15 | 300 | 90,16 | 6 | Zona de temperatura derretida 3 |
| 16* | 300 | 90,23 | 5 | Velocidade rotação do parafuso |
| 17 | 300 | 89,96 | 4 | temperatura da injeção |
| 18 | 297 | 79,37 | 3 | temperatura de resfriamento |
| 19 | 244 | 66,64 | 2 | pressão de injeção |
| 20 | 164 | 46,19 | 1 | máquina |
Sumário do modelo
| Preditores totais | 5 |
|---|---|
| Preditores importantes | 5 |
| Número de árvores cultivadas | 300 |
| Número ótimo de árvores | 300 |
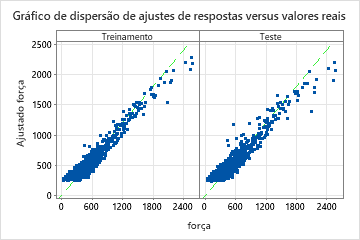
| Estatísticas | Treinamento | Teste |
|---|---|---|
| R-quadrado | 92,23% | 90,23% |
| Raiz do quadrado médio do Erro (RMSE) | 88,8049 | 99,5673 |
| Quadrado médio do erro (MSE) | 7886,3152 | 9913,6420 |
| Desvio absoluto médio (DAM) | 68,9231 | 74,4113 |
| Erro percentual absoluto médio (MAPE) | 0,2083 | 0,2175 |