Observação
Este comando está disponível com o Módulo de análise preditiva. Clique aqui saber mais sobre como ativar o módulo.
Uma equipe de pesquisadores quer usar dados sobre um mutuário e a localização de um imóvel para predizer o valor de uma hipoteca. As variáveis incluem a renda, raça e sexo do mutuário, bem como a localização do setor censitário do imóvel, e outras informações sobre o mutuário e o tipo de imóvel.
Após a exploração inicial para Regressão CART® identificar os preditores importantes, a equipe agora considera Regressão TreeNet® como uma etapa de acompanhamento necessária. Os pesquisadores esperam obter mais informações sobre as relações entre a resposta e os preditores importantes e predizer novas observações com maior exatidão.
Esses dados foram adaptados com base em um conjunto de dados públicos contendo informações sobre hipotecas de bancos federais de empréstimos imobiliários. Dados originais de fhfa.gov.
- Abra o conjunto de dados de amostra HipotecasCompradas.MTW.
- Selecione .
- Em Resposta, digite Valor do empréstimo.
- Em Preditores contínuos, digite Renda Anual – Renda da área.
- Em Preditores categóricos, digite Comprador de casa pela primeira vez – Área estatística baseada em núcleo.
- Clique em Validação.
- Em Método de validação, selecione Validação cruzada de K dobras.
- Em Número de dobras (K), insira 3.
- Clique em OK em cada caixa de diálogo.
Interpretar os resultados
Para esta análise, o Minitab cultiva 300 árvores e o número ótimo de árvores é de 300. Como o número ótimo de árvores está próximo ao número máximo de árvores cultivadas pelo modelo, os pesquisadores repetem a análise com mais árvores.
Sumário do modelo
| Preditores totais | 34 |
|---|---|
| Preditores importantes | 19 |
| Número de árvores cultivadas | 300 |
| Número ótimo de árvores | 300 |
| Estatísticas | Treinamento | Teste |
|---|---|---|
| R-quadrado | 94,02% | 84,97% |
| Raiz do quadrado médio do Erro (RMSE) | 32334,5587 | 51227,9431 |
| Quadrado médio do erro (MSE) | 1,04552E+09 | 2,62430E+09 |
| Desvio absoluto médio (DAM) | 22740,1020 | 35974,9695 |
| Erro percentual absoluto médio (MAPE) | 0,1238 | 0,1969 |
Exemplo com 500 árvores
- Selecione Ajustar hiperparâmetros nos resultados.
- Em Número de árvores, insira 500.
- Clique em Exibir resultados.
Interpretar os resultados
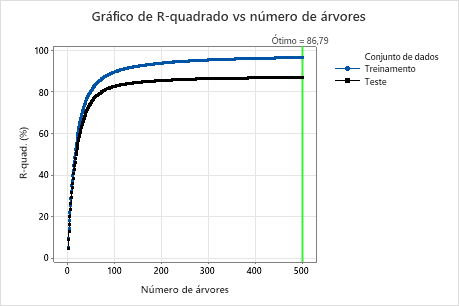
Para esta análise, foram cultivadas 500 árvores e o número ideal de árvores para a combinação de hiperparâmetros com o melhor valor do critério de precisão é 500. A fração da subamostra muda para 0,7 em vez de 0,5 na análise original. A taxa de aprendizado muda para 0,0437 em vez de 0,04372 na análise original.
Examine tanto a tabela sumário do modelo quanto o gráfico R-quadrado versus número de árvores. O valor de R2 quando o número de árvores é 500 é de 86,79% para os dados de teste e é de 96,41% para os dados de treinamento. Esses resultados mostram melhora em relação a uma análise de regressão tradicional e uma Regressão CART®.
Método
| Função de perda | Erro quadrado |
|---|---|
| Critério para seleção do número ótimo de árvores | R-quadrado máximo |
| Validação do modelo | Validação cruzada de 3 dobras |
| Taxa de aprendizado | 0,04372 |
| Fração da subamostra | 0,5 |
| Nós máximos terminais por árvore | 6 |
| Tamanho mínimo do nó terminal | 3 |
| Número de preditores selecionados para divisão de nós | Número total de preditores = 34 |
| Linhas usadas | 4372 |
Informações da Resposta
| Média | DesvPad | Mínimo | Q1 | Mediana | Q3 | Máximo |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
Método
| Função de perda | Erro quadrado |
|---|---|
| Critério para seleção do número ótimo de árvores | R-quadrado máximo |
| Validação do modelo | Validação cruzada de 3 dobras |
| Taxa de aprendizado | 0,001; 0,0437; 0,1 |
| Fração da subamostra | 0,5; 0,7 |
| Nós máximos terminais por árvore | 6 |
| Tamanho mínimo do nó terminal | 3 |
| Número de preditores selecionados para divisão de nós | Número total de preditores = 34 |
| Linhas usadas | 4372 |
Informações da Resposta
| Média | DesvPad | Mínimo | Q1 | Mediana | Q3 | Máximo |
|---|---|---|---|---|---|---|
| 235217 | 132193 | 23800 | 136000 | 208293 | 300716 | 1190000 |
Otimização de hiperparâmetros
| Modelo | Número ótimo de árvores | R-quadrado (%) | Desvio absoluto da média | Taxa de aprendizado | Fração da subamostra | Máximo de do nós terminais |
|---|---|---|---|---|---|---|
| 1 | 500 | 36,43 | 82617,1 | 0,0010 | 0,5 | 6 |
| 2 | 495 | 85,87 | 34560,5 | 0,0437 | 0,5 | 6 |
| 3 | 495 | 85,63 | 34889,3 | 0,1000 | 0,5 | 6 |
| 4 | 500 | 36,86 | 82145,0 | 0,0010 | 0,7 | 6 |
| 5* | 500 | 86,79 | 33052,6 | 0,0437 | 0,7 | 6 |
| 6 | 451 | 86,67 | 33262,3 | 0,1000 | 0,7 | 6 |
Sumário do modelo
| Preditores totais | 34 |
|---|---|
| Preditores importantes | 24 |
| Número de árvores cultivadas | 500 |
| Número ótimo de árvores | 500 |
| Estatísticas | Treinamento | Teste |
|---|---|---|
| R-quadrado | 96,41% | 86,79% |
| Raiz do quadrado médio do Erro (RMSE) | 25035,7243 | 48029,9503 |
| Quadrado médio do erro (MSE) | 6,26787E+08 | 2,30688E+09 |
| Desvio absoluto médio (DAM) | 17309,3936 | 33052,6087 |
| Erro percentual absoluto médio (MAPE) | 0,0930 | 0,1790 |
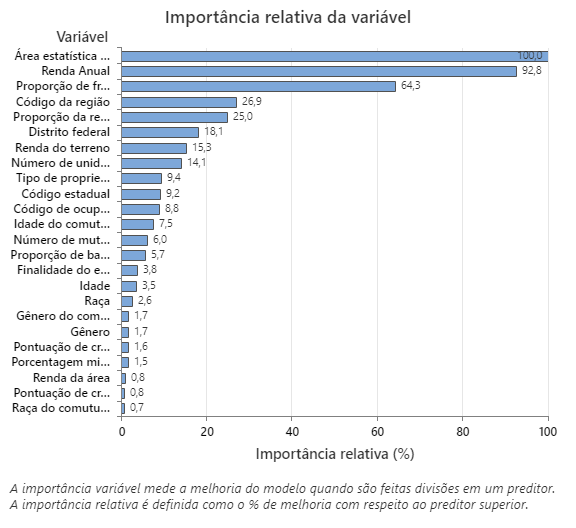
O gráfico de importância relativa da variável representa os preditores por ordem de seu efeito sobre a melhoria do modelo quando as divisões são feitas em um preditor sobre a sequência de árvores. A variável preditora mais importante é a Área Estatística Baseada em Núcleos. Se a importância da variável preditora superior, a Área Estatística Baseada em Núcleos, for 100%, então a próxima variável importante, Renda anual, tem uma contribuição de 92,8%. Isso significa que a renda anual do mutuário é 92,8% tão importante quanto a localização geográfica do imóvel.
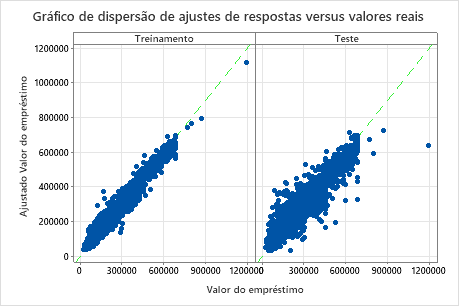
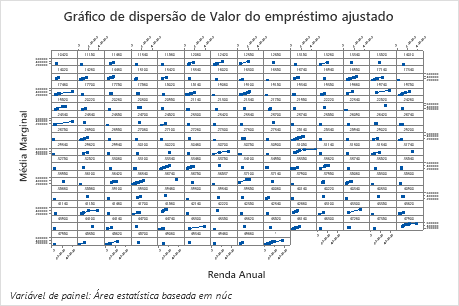
O gráfico de dispersão de valores ajustados de empréstimos versus valores reais de empréstimo mostra a relação entre os valores ajustados e reais tanto para os dados de treinamento quanto para os dados de teste. Você pode passar o mouse sobre os pontos no gráfico para ver mais facilmente os valores representados graficamente. Neste exemplo, todos os pontos ficam aproximadamente perto da linha de referência de y=x.
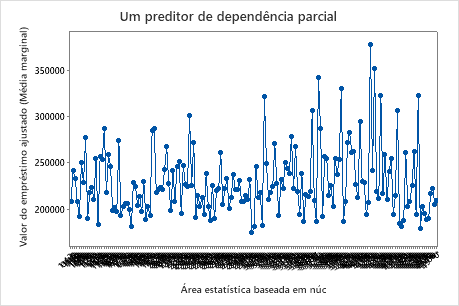
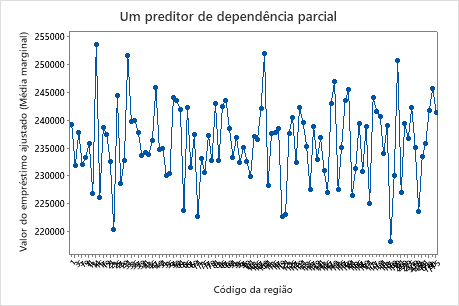
Use os gráficos de dependência parcial para obter uma visão de como as variáveis importantes ou pares de variáveis afetam a resposta predita. Os gráficos de dependência parcial mostram se a relação entre a resposta e uma variável é linear, monotônica ou mais complexa.
O primeiro gráfico ilustra o valor do empréstimo ajustado para cada área estatística baseada em núcleos. Como há tantos pontos de dados, você pode passar o mouse sobre cada um dos pontos de dados para ver os valores específicos de x e y. Por exemplo, o ponto mais alto do lado direito do gráfico é para a área de núcleo número 41860 e o valor do empréstimo ajustado é de aproximadamente US$ 378.069.
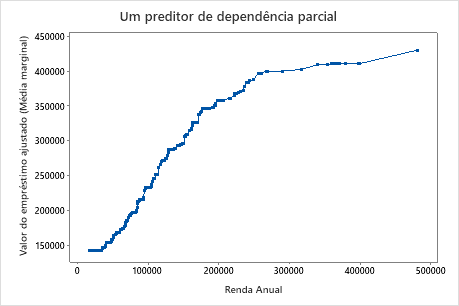
O segundo gráfico mostra que o valor do empréstimo ajustado aumenta à medida que a renda anual aumenta. Depois que a renda anual atinge US $ 300.000, os níveis de valor do empréstimo adequado aumentam a uma taxa mais lenta.
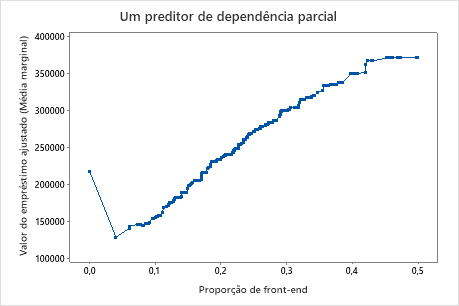
O terceiro gráfico mostra que o valor do empréstimo ajustado aumenta à medida que aumenta a relação de front-end.
O quarto gráfico ilustra o valor do empréstimo ajustado para cada código de condado do censo. Assim como no primeiro gráfico, você pode passar o mouse sobre determinados pontos de dados para obter mais informações. Selecione ou para produzir gráficos para outras variáveis.
